
Współczesne fasady nowoczesnych budynków reprezentacyjnych oprócz funkcji użytkowych w większości przypadków stanowią o wizualnym efekcie obiektu (rys. 1).
Coraz bardziej atrakcyjne stają się fasady z widoczną, czy wręcz eksponowaną konstrukcją metalową, której wrażenia lekkości dodają układy stężeń poprzecznych, układy blacho-kratownic czy kratownic przestrzennych. Coraz popularniejszymi stają się obecnie w tym segmencie budownictwa tzw. kratownice cięgnowe. Wszystkie te układy wykorzystują jako mocowania okładzin połączenia punktowe (rys. 2).
Najlepszą współpracę pomiędzy konstrukcją metalową a kruchym szkłem zapewniają połączenia z wykorzystaniem elastycznych i jednocześnie sprężystych sklein. Połączenie klejone w tych konstrukcjach eliminuje punktowe dociski metalu do tafli szklanej, kruche pękanie szkła, konieczność obróbki (owiercania tafli szklanych), dając wrażenie lekkości i gładkości struktury zewnętrznej budynku.
 Wprowadzenie
Wprowadzenie
W celu podkreślenia reprezentacyjnego charakteru nowobudowanych obiektów, wraz z zastosowaniem konstrukcji kratowych (rys. 2) wykonuje się przeszklenia strukturalne – punktowe, z wykorzystaniem klejonych połączeń stalowych elementów do powłoki szkła. Wymiary tafli szklanych osiągają nawet 5x2,5 m, co tworzy wrażenie niewyobrażalnej wiotkości i lekkości ściany czy przekrycia.
Wiotkość tego typu konstrukcji jest jednak tylko pozorna. Przekrycia te (przeszklenia) odpowiadają takim samym rygorom odnośnie granicznych wartości infiltracji powietrza i wody jak tradycyjne elewacje ścienne.
Sztywność ścian i ich konstrukcji zatem, z uwagi na lokalne podparcia punktowe i styki (uszczelnienia) pomiędzy taflami szkła, musi być zachowana i dokładnie wyznaczona na etapie projektowania konstrukcji.
Wybrane zagadnienia połączeń klejonych
Analiza rozkładu naprężeń
Na obecnym etapie analizy stanu wiedzy trudno jest dobrać jeden algorytm pozwalający na określenie wartości granicznych nośności połączeń, przy uwzględnieniu wszystkich zjawisk mających wpływ na zniszczenie połączenia klejonego.
Specyfika skleiny, charakter jej pracy w różnych etapach obciążenia powodują, że aby oszacować nośność takiego połączenia należy korzystać z kilku modeli materiałowych przy wykorzystaniu Metody Elementów Skończonych. Jest to skutek bardzo złożonej i trudnej w opisie struktury skleiny, opartej na wiązaniach  chemicznych. Dla określenia rozkładu naprężeń w skleinie oparto się na badaniach rozciągania osiowego i modelowania tego zjawiska w programie Ls-Dyna. Dobór modelu materiałowego dla analizy numerycznej rozpoczęto na podstawie określenia modelu reologicznego skleiny (rys. 3).
chemicznych. Dla określenia rozkładu naprężeń w skleinie oparto się na badaniach rozciągania osiowego i modelowania tego zjawiska w programie Ls-Dyna. Dobór modelu materiałowego dla analizy numerycznej rozpoczęto na podstawie określenia modelu reologicznego skleiny (rys. 3).
Skupiono się na modelach materiałowych z grupy polimerów. Wielu badaczy uważa, że ze względu na właściwości mechaniczne polimery można podzielić na trzy klasy: materiały termoplastyczne, termoutwardzalne i chemoutwardzalne (gumy). Podział niniejszy przytoczono na podstawie opracowania [1].
Najbardziej złożoną strukturę z punktu widzenia opisu mechanicznego stanowią termoplastiki, które są zbudowane z długich łańcuchów molekularnych luźno powiązanych ze sobą. Dzięki takiej strukturze łańcuchy molekularne mogą względnie swobodnie wzajemnie przesuwać się i obracać. W gumach, a w szczególności materiałach termoutwardzalnych, występują połączenia chemiczne między łańcuchami molekularnymi, zmieniające właściwości mechaniczne tych materiałów w stosunku do termo-plastików.
W oparciu o powyższe założenia i badania laboratoryjne nad tymi połączeniami do analizy stanu naprężenia wybrano model materiałowy Arruda-Boyce [2], zaczerpnięty z biblioteki programu Ls-Dyna a opracowany w MIT (Massachusetts Institute of Technology) dla hipersprężystych materiałów gumopodobnych, z uwzględnieniem liniowej wiskosprężystości. Jest to jeden z wielu modeli materiałowych opartych na założeniach mechaniki statystycznej, z uwzględnieniem skończonych odkształceń łańcuchów molekularnych, zgodnie z założeniami podanymi przez Bois P. A [3] i M. Puso [4].
W modelach tych jako uproszczenie przyjmuje się topologię układu łańcuchów molekularnych. Model Arruda-Boyce jest modelem opartym na hipotetycznym połączeniu ośmiu takich łańcuchów, zgodnie z założeniami opracowania [4].
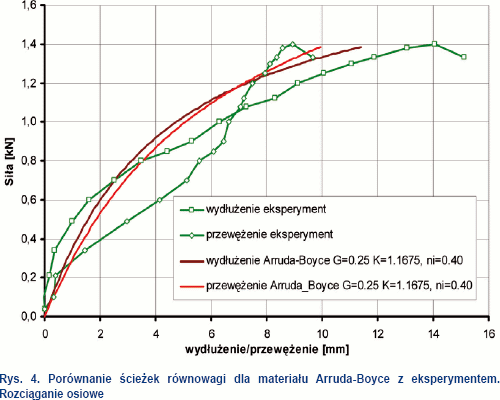
Powyżej przedstawiono wyniki analizy numerycznej i rozkład naprężeń z próby rozciągania modeli materiałowych tej samej skleiny, według założeń modelu materiałowego Arruda-Boyce (rys. 4). Z map naprężeń i geometrii przewężanego modelu widać rozkład i koncentrację naprężeń. Największe niejednorodności i koncentracje występują w pobliżu krawędzi próbki, tam też są ekstremalne wartości naprężeń stycznych. Większe zróżnicowanie wartości naprężeń i przybliżenie punktów koncentracji naprężenia pokrywa się z wartościami otrzymywanymi podczas badań. O właściwym wyznaczeniu punktów koncentracji naprężeń według modelu materiałowego ArrudaBoyce, świadczyć mogą na tym etapie schematy i sposoby zniszczenia badanych modeli połączeń w skleinie. Odrywanie się skleiny na obrzeżach badanych połączeń i obserwacja schematów zniszczenia inicjowanych na styku okładziny lub okucia metalowego ze skleiną, pozwalają na stwierdzenie zgodności ze schematami przedstawionymi na mapach naprężeń pokazanych na rys. 5. Porównywany model Blatz-Ko jest modelem materiałowym standardowo wykorzystywanym dla polimerów w oprogramowaniu Ls-Dyna.
Na tym etapie badań podjęto próbę optymalnego kształtowania skleiny mogącej zniwelować miejsca koncentracji naprężeń i bardziej równomiernie rozłożyć wartości naprężeń, podnosząc nośność całego połączenia. W dalszych etapach badań zajęto się tym zagadnieniem i uzyskane wyniki potwierdziły przypuszczenia o możliwości wzrostu wartości naprężenia średniego w skleinie (odpowiednio każdej składowej tego naprężenia). Uzyskane wyniki zdają się być bardzo obiecujące, ponieważ wzrost wartości naprężeń, a przez to siły niszczącej, sięga nawet 70 do 100%. Jednak na tym etapie zaobserwowano, że w przypadku optymalizacji kształtu skleiny, schemat jej zniszczenia staje się bardziej gwałtowny.
Zjawisko to wymaga głębszej analizy a otrzymane wyniki dokładnego sprawdzenia. Otrzymujemy bowiem większe wartości naprężeń w skleinie ale z uwagi na gwałtowniejszy przebieg zniszczenia większy wpływ zaczynają mieć nawet niewielkie wady połączeń w postaci wtrąceń pęcherzy powietrza czy nieciągłości skleiny. Opis wad w skleinach, zarówno powstałych w sposób mechaniczny, jak i technologiczny podczas procesu układania silikonu oraz procesu jego wiązania, i ich wpływu na nośność połączenia stał się przedmiotem odrębnych rozważań.
Analiza wpływu wad materiałowych na nośność połączeń klejonych
Połączenia badane doświadczalnie wykazywały zróżnicowane wydłużeń, przy których następowało zerwanie. Zerwanie następowało przy całkowitym wydłużeniu od 9 do 15 mm. Przyczyną tego zróżnicowania są prawdopodobnie niejednorodności i wady materiału w postaci pęcherzy powietrza, wtrąceń zanieczyszczeń wewnątrz skleiny lub niedokładności i mechaniczne uszkodzenia na powierzchni materiału. Obserwowano również osłabienie i różnice w pracy skleiny z uwagi niedokładności na styku skleiny z materiałem tafli szklanej, bądź stali.
Na rys. 6 pokazano model połówki próbki z wadą w postaci pustki powietrznej, otrzymanej z usunięcia dwóch elementów przylegających do powierzchni symetrii. Wymiary (x, y, z) całej pustki (należy uwzględnić symetrię) wynoszą 1,04x0,92x0,25 mm. Pustka znajduje się w połowie grubości bryły skleiny, 10,4 mm od krawędzi (rys. 6). Przyjęto model materiału PLP (Piecewise Linear Plasticity) [5]. Jest to jeden z reprezentatywnych przykładów ukrytej wady materiałowej (pęcherz powietrzny). Na jej podstawie przedstawiono wpływ niedokładności połączenia na rozkład naprężeń, ich koncentrację i wpływ zaburzenia na nośność połączenia.
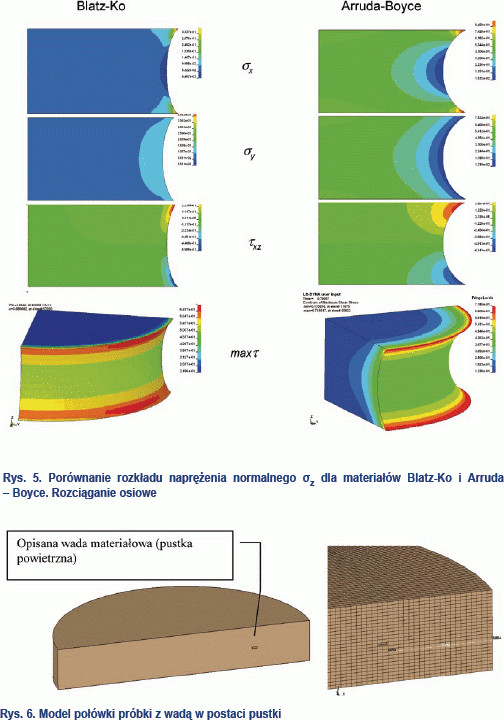
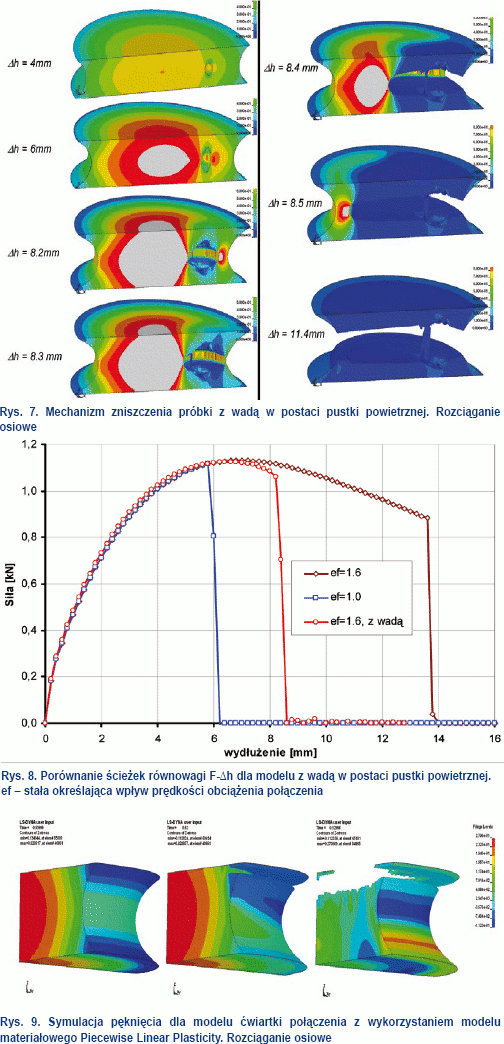
Istnienie wady w postaci pustki powietrznej skutkuje szybszym zniszczeniem próbki. Rozerwanie badanego połączenia z wadą następuje przy wydłużeniu ∆h=8,2 mm, a modelu połączenia bez wady przy wydłużeniu ∆h=13,6 mm. Mechanizm zniszczenia jest wyznaczony z numerycznego modelu połączenia zgodnego z badaniami doświadczalnymi skleiny. Mechanizm powstawania pęknięcia jest uwidoczniony na rys. 7. Sekwencja ujęć w kolejnych momentach obciążenia pokazuje zwiększanie się pustki i propagację pęknięcia.
Mimo wystąpienia dla niektórych elementów wyraźnych deformacji, odpowiadających formom pasożytniczym (hourglass – osiągającym nierzeczywiste odkształcenia pojedynczych elementów skończonych siatki podstawowej skleiny), symulacja komputerowa realistycznie ukazuje mechanizm zniszczenia. Na rys. 7 widać wyraźnie, że miejsca koncentracji naprężeń dla połączeń z wadą ukrytą są inne niż na mapach naprężeń sklein nie posiadających wad zakłócających jednorodność połączenia. Na tym etapie można określić wpływ uszkodzeń na zachowanie się badanych połączeń i podać średnie wartości naprężeń, jakie zostaną przez takie wadliwe połączenia przeniesione, a przy jakich nastąpi ich zniszczenie.
Schemat zniszczenia połączenia wadliwego jest bardzo interesujący z punktu widzenia prowadzonych badań doświadczalnych, potwierdzających fizyczny przebieg zjawiska zniszczenia. Połączenia ze zlokalizowanymi wadami po rozerwaniu potwierdzały swym wyglądem schemat zniszczenia otrzymany w trakcie analizy numerycznego modelu połączenia punktowego. Każde połączenie wykonywane w tej technice może posiadać ukryte wady a ich wpływ na pracę skleiny powinien być szczegółowo określony i zdefiniowany. Należy określić dopuszczalne rodzaje i rozmiary wad, których wpływ na nośność całości połączenia będzie akceptowany dla konstrukcji fasady budynku. Obecnie takiej specyfikacji nie ma, a wady połączeń najczęściej odkrywane są dopiero po wystąpieniu awarii skleiny w połączeniu na budowie.
Specyfika zniszczenia połączeń klejonych
Osiągnięcie modelu zniszczenia w pojedynczym kryterium zniszczenia (pojedynczy element skończony) prowadzi do wyeliminowania tego elementu z dalszych obliczeń w trakcie ich trwania. Dzięki temu można symulować propagację pęknięć w połączeniu, aż do całkowitego zniszczenia, co przedstawiono na rys. 9. Model PLP jest przede wszystkim wykorzystywany dla metali i choć nie jest najbardziej odpowiedni dla polimerów, zwłaszcza przy rozpatrywaniu odciążenia, to jednak zastosowanie go w tym przypadku dla celu poglądowego pokazania mechanizmu zniszczenia połączenia jest jak najbardziej zasadne.
Aby pełniej opisać formę zniszczenia, z wykorzystaniem omawianego modelu materiałowego zajęto się na tym etapie badań różnicowaniem efektywnego odkształcenia plastycznego (1), przy którym następuje zniszczenie.

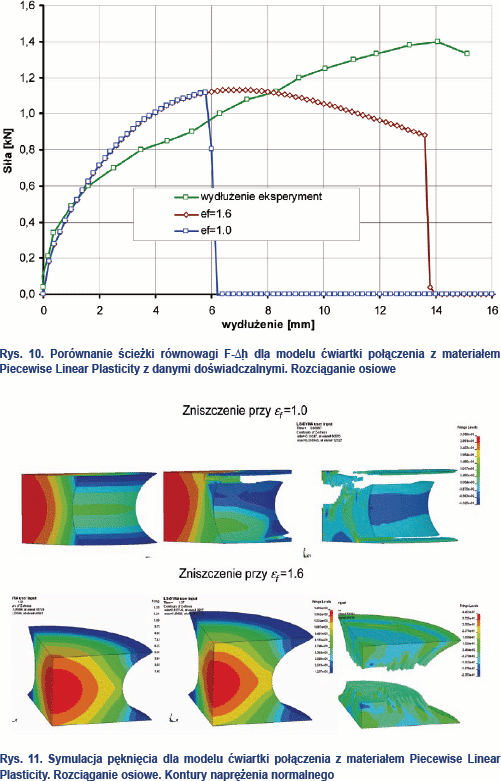
Jest to bowiem bardzo ważny parametr, mający wpływ na formę zniszczenia badanego połączenia (skleiny). Proces zniszczenia połączenia przy uwzględnieniu efektywnego odkształcenia plastycznego przedstawiono na rys. 10 i 11, gdzie na mapach naprężeń przedstawiono stan skleiny przed i w chwili zniszczenia połączenia.
Gwałtowny spadek siły oznacza moment rozerwania próbki, przedstawiono to na rys. 10. Na rysunku tym widać wyraźnie, jak wartość efektywnego odkształcenia przy zerwaniu wpływa na wydłużenie i wartość siły niszczącej rozważanego połączenia. Wielkość efektywnego odkształcenia przy zerwaniu nie wpływa na przebieg ścieżki równowagi, ale powoduje, że przy zadanych warunkach doświadczalnych ścieżka równowagi w trakcie zerwania ulega załamaniu. Na rys. 11 natomiast zobrazowano otrzymane typy zniszczenia połączeń przedstawionych na rys. 10, z wykorzystaniem materiału o charakterystyce Piecewise Linear Plasticity. Widać wyraźnie, jak duże jest zróżnicowanie postaci zniszczenia w zależności od wielkości założonego εf (we wzorze 1 opisanego jako
![]()
Dla mniejszej wartości εf szybciej pojawiające się zniszczenie polega na powstaniu dwóch pęknięć w pobliżu płaszczyzny styku sklejonego z łączonymi elementami skleiny. Jest to tym bardziej ważne, że przy różnych εf powstają w badanym elemencie inne miejsca koncentracji naprężenia. W wypadku mniejszych wartości εf pęknięcia inicjują się na powierzchni bocznej, gdzie są największe odkształcenia w początkowej fazie obciążenia. Całkowite pomierzone wydłużenie przy mniejszej z analizowanych wartości założonego efektywnego odkształcenia wynosiło ok. 5,6 mm. Dla większej wartości εf=1,6 zniszczenie następuje w środku grubości, w miejscu największego przewężenia.
Na rys. 11 pokazano obszary, w których wyeliminowano, w wyniku osiągnięcia przez odkształcenie plastyczne ekstremalnej wielkości, εf ustalonej jako kryterium zniszczenia. Jest to zgodne z założeniami odnośnie matematycznego modelu materiałowego Piecewise Linear Plasticity, mówiącymi, iż przekroczenie wartości naprężeń powodujących uwolnienie (rozpojenie) elementów modelu PLP powoduje ich nadmierne odkształcenie i automatyczne wymazanie.
Politechnika Warszawska
Bibliografia
[1] Berstad T., Clausen A. H., Melve B., Implementation of Constitutive Model for Thermoplastics with Some Preliminary Results, 9th International LS-DYNA Users Conference, Bamberg 2006.
[2] Arruda E. and M. Boyce, A Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials, “Journal of the Mechanics and Physics of Solids”, Vol. 41, No. 2, 1993.
[3] Bois P. A., A simplified approach to the simulation of rubber – like materials under dynamic loading, 4th Euroeans Ls-Dyna Users Conference, May, Ulm, Germany 2003.
[4] Puso M., Mechanistic constitutive models for rubber elasticity and viscoelasticity, Lawrence Livermore National Laboratory. Livermore 2003.
[5] Ls-Dyna Keyword User’s Manual, Livermore Software Technology Corporation, Version 970, April 2003































