Wymagania architektoniczne stawiane współczesnym ścianom osłonowym wymuszają stosowanie oryginalnych rozwiązań konstrukcyjnych. Obecnie bardzo popularne jest stosowanie przeziernych elementów wsporczych, tzw. żeber, do konstrukcji ścian osłonowych (rys. 1), działowych, stropów i zadaszeń szklanych.
Żebra szklane: to nie takie proste
Żebra szklane są to elementy nośne, wykonane ze szkła litego lub klejonego, przejmujące obciążenia od odziaływań obciążeń środowiskowych (wiatr, śnieg) stałych i technologicznych. Żebra zastępują tradycyjne konstrukcje wsporcze, tj. słupy, belki i kratownice. Projektowanie żeber szklanych (w odróżnieniu od tradycyjnych konstrukcji) nie jest zadaniem łatwym. Problemy projektowe mają kilka ważnych aspektów technicznych i obliczeniowych.

Rys. 1. Żebra szklane ściany osłonowej (źródło http://www.charles-henshaw.com)
W zakresie technicznym niezwykle istotnym zagadnieniem jest dobór odpowiednich okuć i węzłów oraz ich montaż. Zagadnienia obliczeniowe (ujęte w niniejszym artykule) sprowadzają się do wyznaczenia prawidłowej pracy statycznej i wytrzymałościowej. W wyniku oddziaływań obciążeń, żebra poddawane są złożonym stanom obciążeń, tj. zginanie, ściskanie, ścinanie. Z uwagi na to, że żebra są to elementy smukłe ze swobodnymi krawędziami, oprócz klasycznych analiz statycznych, niezbędne jest przeprowadzenie obliczeń stateczności. Elementy smukłe poddane ściskaniu i/lub zginaniu wykazują skłonność do wyboczenia, które prowadzi do utraty stateczności przed przekroczeniem wytrzymałości na zginanie. Przykład analizy obrazującej te zjawiska przedstawiono poniżej.
Analizowano żebro szklane rozpiętości 3,0 m, szerokości 0,25 m, z szyby litej 12 mm. Żebro podparte jest przegubowo wzdłuż krótszych krawędzi (rys. 2). Obciążenie przyłożone jest do czoła, wzdłuż płaszczyzny żebra. Przeprowadzono obliczenia numeryczne, w których wyznaczono obciążenie krytyczne przy zginaniu dla pierwszej postaci wyboczenia oraz naprężenia i przemieszczenia, z uwzględnieniem imperfekcji geometrycznych, wywołanych pierwszą postacią wyboczenia.
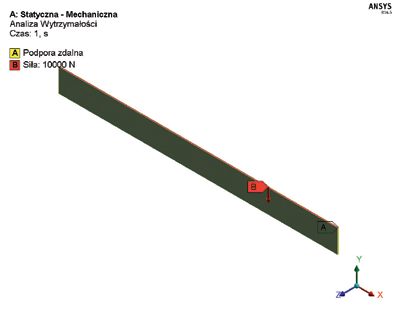
Rys. 2. Model obliczeniowy
Na rys. 3 przedstawiono mapę naprężeń zredukowanych wraz z deformacją żebra. Maksymalne naprężenia wynoszą 31,5 MPa i nie przekraczają naprężeń dopuszczalnych dla szkła hartowanego (50 MPa). Zatem w przypadku analizy wytrzymałościowej, przy uwzględnieniu kryterium naprężeniowego nośność wykorzystana jest zaledwie w ok. 60%. Analizując dalej ten sam przykład, ale przy uwzględnieniu wyboczenia okazuje się, że pierwsza (decydująca o stateczności) postać wyboczenia występuje przy współczynniku siły 0,94, tj. przy sile 9,4 kN. Oznacza to, że stateczność żebra została utracona przed osiągnieciem pierwotnej siło 10 kN powodującej powstanie naprężeń o wartości 31,5 MPa. Na rys. 4 przedstawiono wyniki obliczeń oraz pierwszą postać wyboczenia.
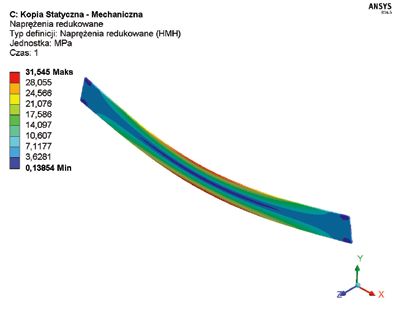
Rys. 3. Naprężenia zredukowane
(...)
Najbardziej efektywnym narzędziem w ocenie nośności i stateczności są obliczenia numeryczne. Obliczenia takie powinny być wykonane z wykorzystaniem odpowiedniej klasy oprogramowania.
Niestety, projektanci nie zawsze mają dostęp do takiego oprogramowania. Oprócz numeryki istnieją „klasyczne” metody projektowania żeber szklanych z uwzględnieniem efektów utraty stateczności.
Taką metodę przedstawiono w przytoczonym w bibliografii opracowaniu [1]. Skrótową wersję metody projektowania na tej podstawie przedstawiono w dalszej części artykułu.
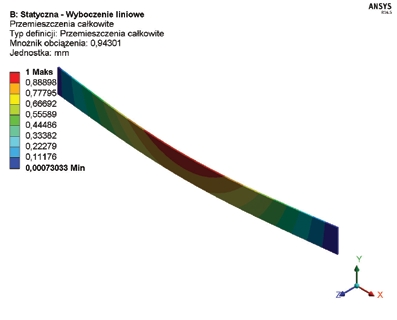


Rys. 4. Wynik obliczeń i mapa pierwszej postaci wyboczenia
Projektowanie żeber szklanych
Żebra narażone są na globalną utratę stateczności przy oddziaływaniu obciążeń podłużnych oraz poprzecznych.
Przy projektowaniu żeber szklanych należy sprawdzić:
a) warunki nośności przy oddziaływaniu sił podłużnych i momentów gnących,
b) warunki stateczności przy wyboczeniu giętnym oraz skrętnym.
Wyboczenie giętne [1]
W przypadku ściskania mimośrodowego żebra, naprężenia należy wyznaczać wg zależności:
![]() (1)
(1)
gdzie:
N – wartość przyłożonej siły ściskającej,
M – wartość momentu zginającego z uwzględnieniem efektów II rzędu,
wmax – maksymalne ugięcie w środku tafli z uwzględnieniem efektów II rzędu,
wo – początkowe ugięcie w środku tafli,
e – mimośród przyłożonej siły,
Ac– pole przekroju poprzecznego żebra,
W – wskaźnik wytrzymałości przekroju żebra w kierunku
zginania W=bt2/6.
Siła krytyczna przy ściskaniu żebra ze szkła litego wyznaczana jest wg zależności:
![]() (2)
(2)
gdzie:
E – moduł Younga szkła
I – moment bezwładności litego przekroju tafli żebra w kierunku zginania,
Lcr – długość wyboczeniowa żebra (równa długości teoretycznej L w przypadku podparcia przegubowego) dla układu jednoprzęsłowego bez stężeń pośrednich.
Maksymalne ugięcie w środku tafli z uwzględnieniem efektów II rzędu:
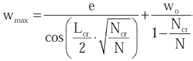 (3)
(3)
Ncr – wartość siły krytycznej,
N – wartość przyłożonej siły ściskającej,
e – mimośród przyłożonej siły (dane z projektu),
Lcr – długość wyboczeniowa tafli (równa długości tafli),
wo – początkowe ugięcie w środku tafli,
w=bt2/6 – efektywny wskaźnik wytrzymałości dla szyby,
b – szerokość żebra,
t – grubość żebra.
W przypadku ściskania mimośrodowego żebra ze szkła klejonego, siłę krytyczną wyznacza się wg zależności:
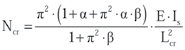 (4)
(4)
Is – moment bezwładności przy skręcaniu
E – moduł Younga szkła
Lcr – długość wyboczeniowa tafli (równa długości tafli)
Dla żebra klejonego z dwóch tafli szkła:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Dla żebra klejonego z trzech tafli szkła:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
gdzie:
I1 – moment bezwładności tafli 1,
I2 – moment bezwładności tafli 2,
z1, z2, t1, t2, t3, tint – pokazano na rysunku 5,
Gint – moduł Kirchoffa warstwy wewnętrznej szyby (o wartości maksymalnie do 4,0 GPa).
Równoważna grubość żebra klejonego (z dwóch lub trzech tafli szkła):
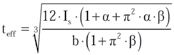 (11)
(11)
Is – moment bezwładności przy skręcaniu,
α, β – jak wyżej..
Efektywny wskaźnik wytrzymałości żeber klejonych:
![]() (12)
(12)
b – szerokość panelu,
teff – równoważna grubość panelu.
Warunek odporności tafli na wyboczenie jest aby maksymalne naprężenie przy ściskaniu mimośrodowym, nie przekraczało naprężeń efektywnych dla szkła :
![]() (13)
(13)
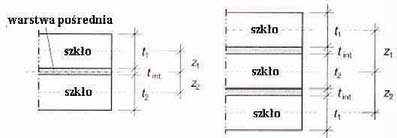
Rys. 5. Oznaczenie grubości tafli klejonych
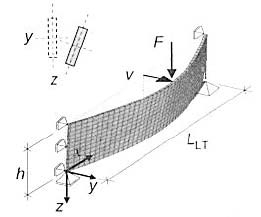
Rys. 6. Schemat wyboczenia skrętnego [1]
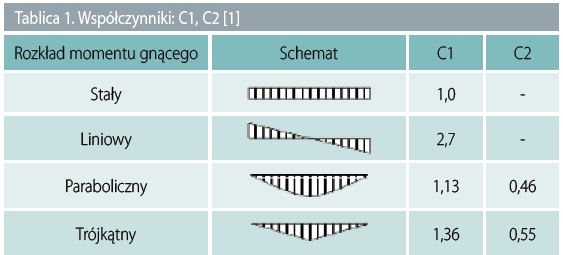
Tablica 1. Współczynniki: C1, C2 [1]
Wyboczenie skrętne [1]
Wyboczenie skrętne występuje w żebrze poddawanym zginaniu w płaszczyźnie prostopadłej do osi wzdłużnej elementu. Taki sposób obciążenia występuje w przypadku belek zginanych, płatwi dachowych i usztywnień poprzecznych ścian osłonowych. Typowy przykład wyboczenia skrętnego elementu jednoprzęsłowego przedstawia rys 6.
Moment krytyczny, przy którym następuje poprzeczna utrata stateczności wyznacza się wg zależności:
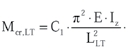
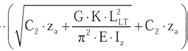 (14)
(14)
E – moduł Younga szkła,
G – moduł Kirchoffa szkła,
K – stała skręcania,
LLT – długość tafli,
Iz – moment bezwładności względem osi z (wg rys. 6),
za – odległość pomiędzy środkiem ciężkości tafli i punktem przyłożenia obciążenia,
C1, C2 – współczynniki uwzględniające rozkład momentu gnącego wg tablicy 1.
Stała skręcania dla przekrojów prostokątnych wyznacza się w zależności od wymiarów poprzecznych żebra (szerokość b i wysokość h)
![]() (15)
(15)
Sprowadzona sztywność przy zginaniu żebra ze szkła klejonego:
![]() (16)
(16)
Is – moment bezwładności przy skręcaniu,
E –moduł Younga szkła.
Współczynnik α, β i moment bezwładności Is wynosi:
– dla szyby klejonej z dwóch tafli:
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
– dla szyby klejonej z trzech tafli:
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
I1 – moment bezwładności tafli 1,
I2 – moment bezwładności tafli 2,
z1, z2, t1, t2, t3, tint – pokazano na rysunku 5.
Zastępcza sztywność na skręcanie pakietu klejonego określa się jako:
![]() (23)
(23)
1) szyba klejona z 2 tafli
2) szyba klejona z 3 tafli
G – moduł Kirchoffa szkła
Ki – stała skręcania i–tej tafli
![]() (24)
(24)
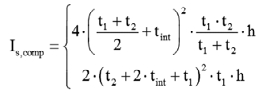 (25)
(25)
1) szyba klejona z 2 tafli
2) szyba klejona z 3 tafli
Smukłość:
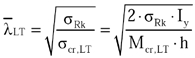 (26)
(26)
σRk – charakterystyczna wytrzymałość na rozciąganie,
σcr, LT – naprężenie krytyczne wyboczenia skrętnego,
Iy – moment bezwładności względem osi y,
h – wysokość panelu,
Mcr, LT – moment krytyczny wg wzoru (57).
Obliczeniowy moment zginający:
![]() (27)
(27)
σRk – obliczeniowa wytrzymałość na rozciąganie.
Wy – wskaźnik wytrzymałości względem osi y. – zależność jak na rysunku 7.
Warunek, który należy spełnić, aby nie wystąpiło wyboczenie skrętne:
![]() (28)
(28)
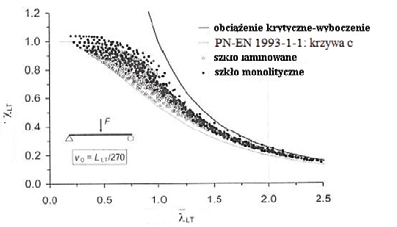
Rys. 7. Współczynniki wyboczeniowe [1]
Podsumowanie
Przy projektowaniu żeber szklanych, oprócz sprawdzenia nośności i ugięć, bardzo istotne jest sprawdzenie warunku stateczności, który decyduje o przydatności danego rozwiązania do zastosowania w praktyce.
Do wykonania kompleksowej analizy bardzo użytecznym narzędziem są numeryczne metody obliczeniowe. Niestety programy numeryczne odpowiedniej klasy są narzędziem drogim i wymagającym zaawansowanej obsługi.
Równie skutecznym narzędziem analiz statycznych są „klasyczne” metody wymiarowania przedstawione w niniejszym artykule. Metody te wymagają dużego nakładu pracy, jednak są dostępne dla projektantów i wyróżniają się dostatecznie dobrą dokładnością.
Literatura
[1] Haldimann, A. Luible, M. Overend. Structural Use of Glass. „Structural Engineering Documents” 10. Iabse–Aipss–Ivbh, ETH Zurich 2008.
dr inż. Artur Piekarczuk
Instytut Techniki Budowlanej
Całość artykułu w wydaniu drukowanym I elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacj: Świat Szkła 05/2014































