Wolnostojące balustrady ze szkła laminowanego pracujące jako wspornik zamocowany w ciągłej podstawie (tzw. „but” – shoe) należą do najczęściej spotykanych zastosowań szkła konstrukcyjnego.
Wytrzymałość szkła laminowanego jest zwykle określana w sposób przybliżony tzw. „metodą efektywnej grubości” opracowaną przez
Bennisona, zaadaptowaną na podstawie teorii kompozytów warstwowych przez Wolfela w celu uzyskania swobodnie podpartej belki pod równomiernie rozłożonym obciążeniem.
Jednak obserwuje się znaczące niedoszacowanie naprężeń przy zastosowaniu sztywnej międzywarstwy strukturalnej (folii laminującej), gdzie wspornikowe szkło laminowane modeluje się jako obciążone wyidealizowanym stałym momentem.
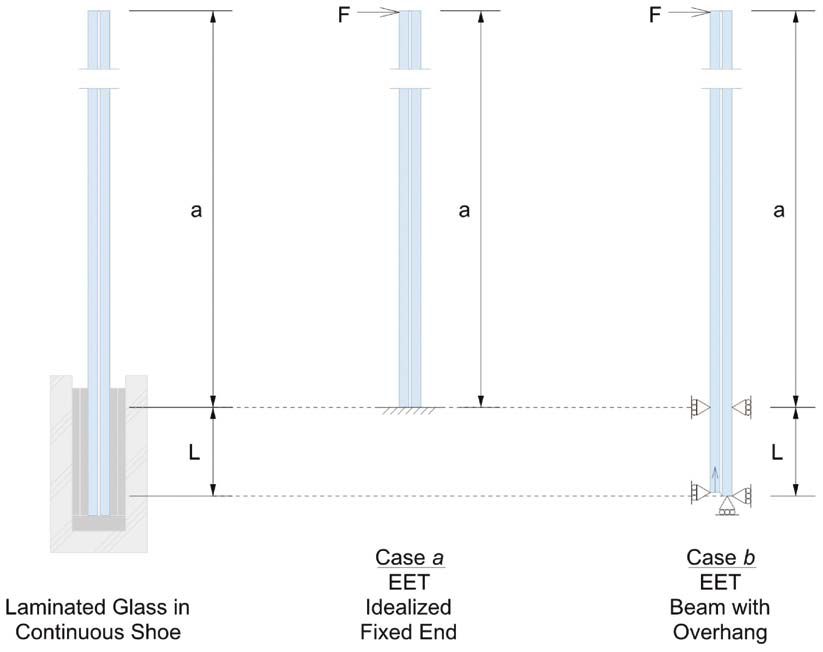
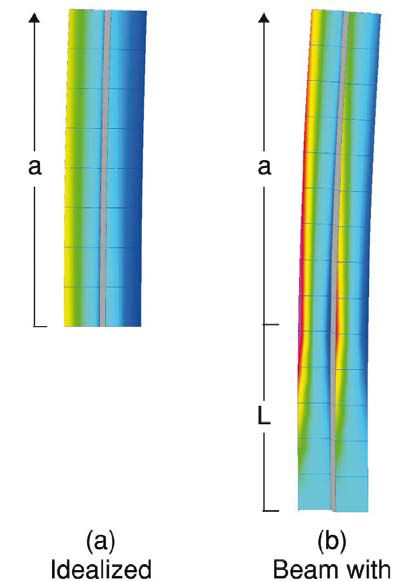
Rys. 1. Rozważane warunki utwierdzenia dla wspornikowego szkła laminowanego poddanego oddziaływaniu obciążenia liniowego: a) wyidealizowany moment utwierdzający, b) wystająca z podpory belka swobodnie podparta
Niniejszy artykuł ma na celu określenie dokładności analizy wspornikowej balustrady ze szkła laminowanego w celu opracowania praktycznej metody projektowania, badając zastosowania ulepszonej metody efektywnej grubości (EET) autorstwa Galuppi i Royer-Carfagni.
Proponowane są tutaj nowe obliczenia dla współczynnika EET dla balustrady ze szkła laminowanego, pracującej jako wspornik zamocowany w ciągłej podstawie.
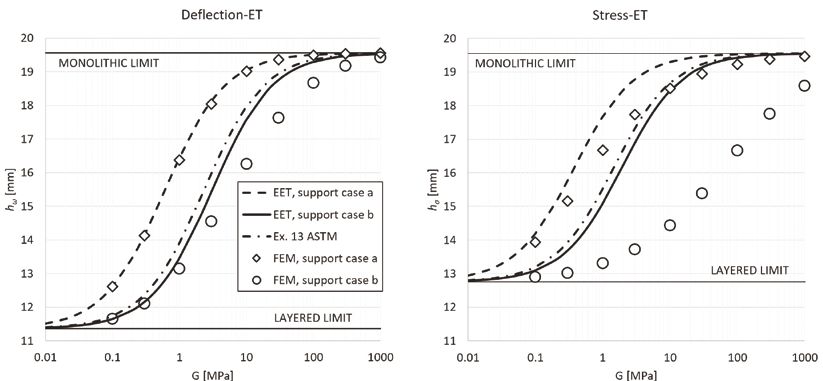
Wytrzymałość wg metody efektywnej grubości przyjętej w normie ASTM E1300 i dwie metody obliczeń EET są porównywane z numerycznymi modelami obliczania naprężeń i ugięć, ze szczególnym uwzględnieniem przykładu 13 z normy ASTM E1300.
Wprowadzenie
Sztywność i wytrzymałość szkła laminowanego (LG), utworzonego z warstw szkła połączonych ze sobą polimerowymi warstwami pośrednimi (foliami laminującymi), polega na sprzężeniu warstw szkła przez międzywarstwę polimeru.
Zwykle wartość nośności znajduje się między dwoma przypadkami granicznymi, określanymi jako wartość graniczna dla niepołączonych warstw (tj. beztarciowe przesunięcie względem siebie warstw szklanych, odpowiadające przypadkowi międzywarstwy bez sztywności), a wartością graniczną dla monolitycznie połączonych warstw (tj. idealne związanie warstw, odpowiadające przypadkowi międzywarstwy z bardzo wysoką sztywnością na ścinanie).
Do celów projektowych bardzo przydatne jest zdefiniowanie grubości efektywnej (ET) szkła laminowanego (LG), tj. grubości równoważnego monolitycznego elementu szklanego o takich samych właściwościach w czasie zginania pod względem naprężenia lub ugięcia. Metody efektywnej grubości znacznie upraszczają obliczenia statyczne konstrukcji ze szkła laminowanego. Literatura i różne normy przedstawiają różne metody obliczania grubości efektywnej (ET).
Zastosowanie metody efektywnej grubości Wolfel-Bennison (W-B) [1], [2] do projektowania wspornikowej balustrady ze szkła laminowanego zamocowanej w ciągłej podstawie jest powszechne akceptowana w literaturze dla przemysłu szklarskiego, przyjęte też w aprobacie technicznej ICC-ES ESR-3842 [3] i wsparte przykładem projektowania w normie ASTM E1300 [4].
Pojawiły się obawy o dokładność tej popularnej metody analizy dla wspornikowej balustrady LG, po porównaniu wyników naprężeń i ugięć obserwowanych w modelach numerycznych dla typowych warunków podparcia.
Aby poprawić dokładność obliczeń i opracować zasady projektowania przeanalizowano zastosowanie ulepszonej metody efektywnej grubości (Enhanced Effective Thickness EET), zaproponowanej przez Galuppi i Royer-Carfagni [6], do odwzorowania wspornikowego podparcia tafli szkła laminowanego w podporze ciągłej. Dokładność metod ET dla obciążenia liniowego jest porównywana z modelami numerycznymi dla różnych warunków podparcia.
Podparcie ciągłe (liniowe)
Wspornikowe balustrady ze szkła laminowanego są zwykle zamocowane w ciągłej (liniowej) podstawie o przekroju profilu U – niekiedy określa się kształt takiej podpory jako kształt stopy lub buta (shoe).
Szkło monolityczne lub szkło laminowane (LG) osadza się w profilu zwykle o głębokości od 70 do 100 mm i aby uniemożliwić obrót utwierdza się metodą mocowania na mokro lub na sucho, odpowiednio przez wstrzyknięcie zaprawy cementowej/żywicy epoksydowej lub punktowe rozmieszczenie bloków klinowych.
Nie zauważa się różnic we właściwościach konstrukcyjnych szkła, zarówno mocowanych na mokro, jak i na sucho, zgodnie ze specyfikacją producenta [3].
Precyzja cyklicznego punktowego podparcia w porównaniu do podparcia ciągłego nie jest analizowana w tym dokumencie, ale wymaga dalszych badań.
Mechanikę pracy wspornikowej balustrady można modelować przy użyciu różnych warunków brzegowych, jak pokazano na rys. 1. Warunki brzegowe wyidealizowane jako moment przykładany w miejscu sztywnego utwierdzenia (a) wymagają opracowania reakcji sił osiowych warstwy szklanej w miejscu podparcia.
Warunki brzegowe wystającej z podpory belki swobodnie podpartej z dwóch stron (b) pozwalają na poślizg między warstwami szkła na podpartym końcu. Osiowe podparcie jest zapewnione dla jednej warstwy szkła, aby zapobiec swobodnemu ruchowi ciała.
Analiza obu warunków podparcia dla monolitycznego szkła daje takie same naprężenia. A dla stosunkowo niewielkiej odległości L między punktami podparcia, w porównaniu do wspornika o długości a, praktycznie identyczne przemieszczenie. Określana w analizie numerycznej, wytrzymałość wspornikowej balustrady ze szkła laminowanego (LG) jest inna dla każdego przykładu wspornikowego podparcia.
Opracowanie idealnego momentu utwierdzającego balustrady ze szkła laminowanego (LG) w zwykłej podporze balustradowej o profilu U wymaga klinów zaciskowych, mocujących na zasadzie tarcia lub adhezji, aby zapobiec ślizganiu się warstw szkła. Youri Baidjoe [5] wykazał, że zwykle elastyczność podpory powoduje niewielki obrót w profilu, jakościowo zmniejszając skuteczność zaciskania lub jednolitość przyczepności. Istnieją konstrukcje, w których poślizgowi można zapobiegać przy najwyższych obciążeniach projektowych.
Należy jednak zwrócić szczególną uwagę na potwierdzenie przyjętych założeń – w tym rozkład sił, zgodność odkształceń i weryfikację parametrów sztywności mocowania – za pomocą kwalifikowanej metody kontroli.
Uwzględniono warunki wsparcia przy modyfikacji metody EET, aby zapewnić dokładniejsze oszacowanie wytrzymałości wspornikowej balustrady ze szkła LG podlegającej obciążeniu liniowemu. Dokonano porównania modeli numerycznych z modelami ET dla różnych warunków brzegowych: (a) wyidealizowanego utwierdzenia i (b) belki swobodnie podpartej.
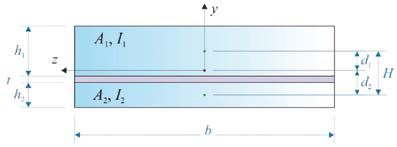
Rys. 2. Przekrój belki ze szkła laminowanego LG złożonej z dwóch szklanych warstw połączonych polimerową warstwą pośrednią.
Metoda efektywnej grubości Wolfel-Bennison (W-B)
Dominujący model ulepszonej efektywnej grubości zaproponowany przez Bennisona [1] jest oparty na oryginalnej pracy Wolfela [2] i przyjęty w normie ASTM E1300 [4].
Aby zilustrować tę metodę, rozważmy belkę o długości L i szerokości b, której przekrój, pokazany na rys. 2, składa się z dwóch zewnętrznych warstw szklanych o grubości h1 i h2 z modułem Younga E, połączonych warstwą polimerową o grubości t i moduł sprężystości na ścinanie G.
Niech:
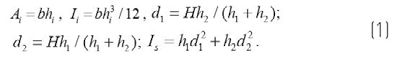
Metoda W-B określa następujący wzór dla obliczania ugięcia i naprężenia dla efektywnej grubości dla pierwszej i drugiej warstwy szkła „i”, odpowiednio:
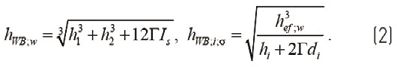
gdzie współczynnik sprzężenia ścinającego „Γ” jest oceniany w odniesieniu do bardzo szczególnego schematu statycznego belek swobodnie podpartych pod równomiernie rozłożonym obciążeniem.
Niemniej jednak wzory te są często używane w obliczeniach numerycznych w celu oszacowania stanu naprężenia i odkształcenia belek i płyt ze szkła laminowanego (LG) dla zwykłych warunków granicznych i obciążenia.
Przykład 13 z normy ASTM E1300 [4] ma na celu zaoferowanie rozwiązania ET dla wspornikowej balustrady z LG poddanej obciążeniu liniowemu zgodnie z metodą efektywnej grubości W-B. Zwiększenie długości międzywarstwy odpowiada wymiarowi wysunięcia wspornika „a”.
To rozwiązanie powoduje słabsze utwierdzenie w porównaniu z wyidealizowanym utwierdzeniem końca wspornika (przypadek a), jednak takie warunki brzegowe są do zaakceptowania w tej adaptacji metody efektywnej grubości W-B dla belek swobodnie podpartych.
Ulepszona metoda efektywnej grubości
Bardziej ogólne sformułowanie, zwane ulepszoną metodą efektywnej grubości (Enhanced Effective Thickness EET), zostało zaproponowane przez Galuppi i Royer-Carfagni [6].
Opiera się ono na podejściu wariacyjnym, które poprzez minimalizację energii odkształcenia znajduje najlepsze przybliżenie dla reakcji szkła laminowanego. Metodę, którą można rozszerzyć na dwuwymiarowy przypadek płyt [7] i wielowarstwowych laminatów [8], wspomniano w przygotowywanym przyszłym Eurokodzie 11 dla szkła konstrukcyjnego [9].
Główne założenia tego modelu to:
- efektywny moment bezwładność pakietu szkła laminowanego (LG) jest średnią ważoną harmoniczną momentu bezwładności związanego z warunkami granicznymi dla modelu monolitycznego i warstwowego;
- dokładną wartość parametru ciężaru można znaleźć poprzez minimalizację energii;
- kształt odkształconej belki LG ma postać elastycznie zakrzywionej monolitycznej belki o stałym przekroju w tych samych warunkach obciążenia i warunkach granicznych.
W przypadku elementów LG wykonanych z dwóch szklanych warstw, ugięcie i naprężenie dla efektywnej grubości można oszacować jako:
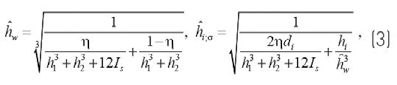
gdzie parametr η, dostosowujący zachowanie od granicy monolitycznej (η = 1) do granicy warstwowej (η = 0), podaje:
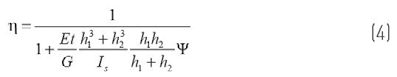
Wytrzymałość okazuje się zależeć od właściwości mechanicznych zarówno szkła, jak i polimeru, właściwości geometrycznych pakietu LG, warunków brzegowych i warunków obciążenia. Wartości współczynnika Ψ są określone w pracy Galuppi, Manara i Royer-Carfagni [10] dla przypadków projektowych o największym znaczeniu praktycznym.
Jak omówiono w pracy Wsporniki balustrad ze szkła laminowanego: zmodyfikowane podejście EET i problemy projektowe [11] dla balustrad i ogólnie dla asymetrycznych schematów statycznych i/lub dla warunków podparcia, w których warstwy szkła mogą się poruszać w kierunku osiowym, model EET należy zmodyfikować, aby uwzględnić możliwość ograniczonego przesunięcia jednej warstwy szkła w stosunku do drugiej.
Mówiąc dokładniej, ilekroć osiowe przemieszczenia dwóch warstw szkła nie są ograniczone aby były takie same w danym punkcie, może wystąpić wzajemne przesunięcie, nie zmieniające stanu naprężenia warstw szkła, ale zmierzające do zminimalizowania energii naprężenia międzywarstwy. Zmniejsza to naprężenie ścinające przenoszone przez międzywarstwę, a w konsekwencji stopień sprzężenia między warstwami szkła i wynikową efektywną grubość belki.
Wartości współczynnika Ψ są uzyskiwane w pracy Wsporniki balustrad ze szkła laminowanego… [11] za pomocą technik minimalizacji energii, dla różnych warunków obciążenia i warunków brzegowych.
W rozpatrywanych przypadkach są to:
Podparcie jako wyidealizowany moment utwierdzający na końcu:
przypadek a

Podpora jako belka wysunięta z podpory:
przypadek b

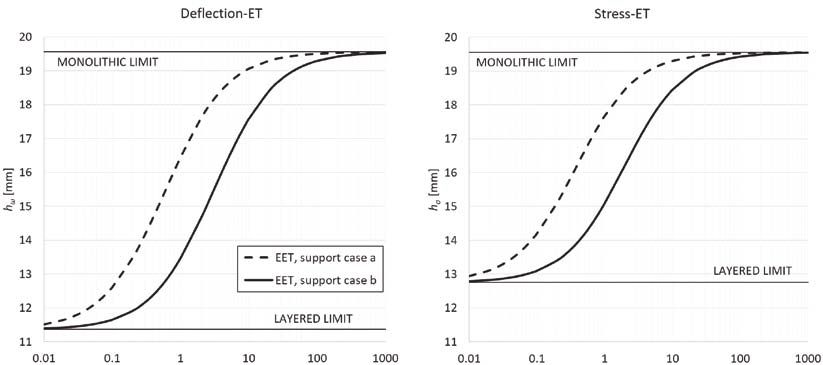
Rys. 3 pokazuje porównanie ugięcia (po lewej stronie) i naprężenia (po prawej stronie) przy grubości efektywnej uzyskanych dla warunków brzegowych dla przypadku (a) i przypadku (b). Uwzględniona geometria jest zdefiniowana przez: h1 = h2 = 9,02 mm, t = 1,52 mm, a = 1100 mm dla wspornika i L = 50 mm dla odległości między punktami podparcia (przypadek b).
Z jakościowego punktu widzenia można zauważyć, że ilekroć dwie warstwy szkła mogą się przemieszczać względem siebie w kierunku osiowym (podparcie przypadek b), sprzężenie na ścinanie zmniejsza się, prowadząc do niższych wartości efektywnej grubości dla danej wartości G.
(...)
Adam Nizich, Walter P. Moore & Associates, Inc.
Laura Galuppi, University of Parma
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. w Tampere w Finlandii
Bibliografia
[1] Calderone, I., Davies, P.S., Bennison, S.J., Xiaokun, H., Gang, L.: Efektywna grubość laminatu przy projektowaniu szkła laminowanego. w: Skrypt konferencyjny GPD 2009 Tampere (FI).
[2] Wolfel, E.: Efektywna grubość kompozytu. Przybliżone rozwiązanie i możliwe zastosowania. W: Stahlbau. (1987) 173–180.
[3] ESR-3842. System podpór balustrady szklanej GRSTM do mocowania laminowanego szkła hartowanego, C.R. Laurence Company, Inc., Raport ewaluacyjny ICC-ES, (3: 2018)
[4] ASTM E1300-16. Standardowa praktyka określania odporności na obciążenia przeszklonych budynków, ASTM International, West Conshohocken, PA (2016)
[5] Baidjoe, Y., i in.: Metody obliczania balustrad szklanych mocowanych w aluminiowych profilach, Glass Struct. Eng., (2018) 3: 321-334
[6] Galuppi, L., Royer-Carfagni, G.: Efektywna grubość laminowanych szklanych belek. Nowe wzory uzyskane poprzez podejście wariacyjne, Ing. Struct., 38 (2012) 53-67.
[7] Galuppi, L., Royer-Carfagni, G.: Skuteczna grubość laminowanych płyt szklanych, J. Mech. Mata. Struct. 7 (2012) 375–400.
[8] Galuppi, L., Royer-Carfagni, G.: Zwiększona efektywna grubość wielowarstwowego szkła laminowanego, kompozyty: część B, 64 (2014) 202–213.
[9] CEN / TC 250. prCEN / TS xxxx 2: 2018 Szkło konstrukcyjne - Zasady projektowania i budowy. Część 2: Elementy szklane obciążone zewnętrznie. (2018)
[10] Galuppi, L., Manara, G., Royer-Carfagni, G.: Praktyczne wyrażenia przy projektowaniu laminatów, Kompozyty: Część B 45 (2013) 1677–1688.
[11] Galuppi, L., Nizich, A.: Wsporniki balustrad ze szkła laminowanego: zmodyfikowane podejście EET i problemy projektowe. W przygotowaniu (2019).
[12] Strand7, 2019. Strand7 Finite Element Software, R3 Preview, Strand7 Pty Limited, Sydney (AU).
[13 ASCE 7-16. Minimalne obciążenia projektowe i powiązane kryteria dla budynków i innych konstrukcji. Amerykańskie Stowarzyszenie Inżynierów Budownictwa. (2017), Reston, VA
[14] NBC-10. National Building Code of Canada. National Research Council of Canada. Ottawa, ON. (2010)
[15] Kuraray. Konstrukcja i bezpieczeństwo: Dane techniczne Trosifol. (10: 2018)
[16] CSA A500-16. Strażnicy budowlani. Grupa CSA. Toronto, ON. (9: 2016)

Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 04/2020