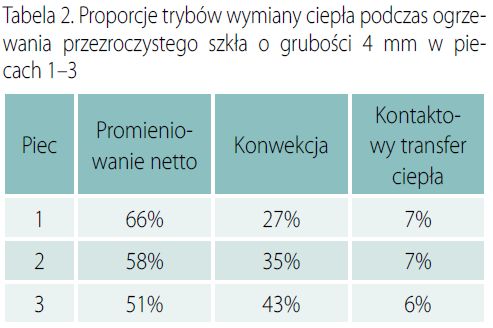
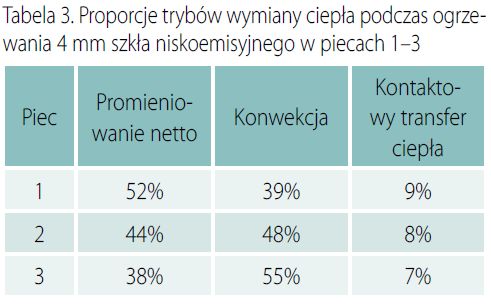
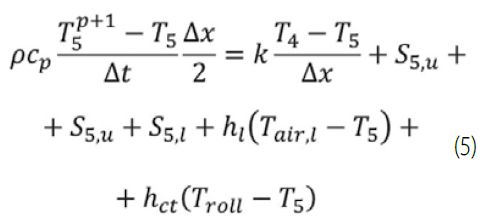W piecu do hartowania szkło jest umieszczane na wierzchu obracających się rolek ceramicznych, gdzie jest wystawione na promieniowanie emitowane przez promienniki, walce i inne powierzchnie wewnątrz pieca. A ciepło przenoszone konwekcyjnie przez strumienie gorącego powietrza, nagrzewa obie szklane powierzchnie. Na dolnej powierzchni zachodzi również kontaktowa wymiana ciepła pomiędzy szkłem a rolkami.
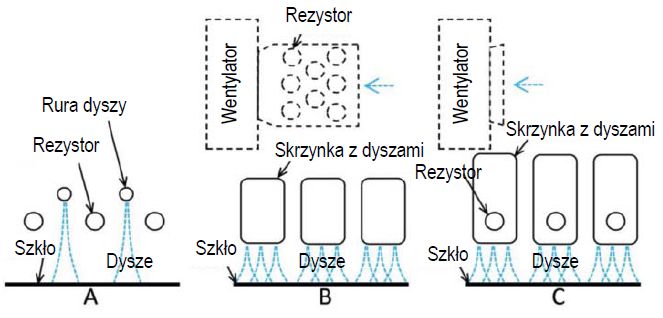
Rys. 1. Różne lokalizacje rezystorów używanych w piecach do hartowania
Na rynku istnieje dość szeroka gama różnych modeli pieców do hartowania szkła z różnorodnymi urządzeniami do realizacji radiacyjnego i konwekcyjnego przenoszenia ciepła. W artykule opisano podstawowe modele/ tryby pracy strumieni ciepła oraz przedstawiono metodę rozwiązania równania energii szkła. Ponadto dokonano teoretycznej analizy działania niektórych pieców do hartowania, aby przedstawić szczegóły zjawisk przenoszenia ciepła wewnątrz nich podczas ogrzewania.
Wstęp
Hartowanie szkła to proces, w którym wytrzymałość szkła float poprawia się poprzez obróbkę cieplną. W piecu do hartowania tafla szkła zostaje umieszczona na obracających się ceramicznych wałkach. Podczas procesu hartowania płyty szklane są podgrzewane do około 640°C, a następnie szkło jest szybko schładzane strumieniami chłodnego powietrza - szybkość chłodzenia zależy od grubości szkła. W idealnym procesie nagrzewania przenikanie ciepła do szkła jest takie samo przez górną i dolną stronę, dzięki czemu profil temperaturowy generowany w szkle podczas ogrzewania jest symetryczny.
Po podgrzaniu, tj. tuż przed hartowaniem (schłodzeniem), temperatura szkła powinna być taka sama na całej powierzchni szkła i taka sama we wszystkich taflach szklanych umieszczonych w piecu. Zdolność pieca do osiągnięcia tak idealnego procesu nagrzewania w oczywisty sposób zależy od jego modelu. W najprostszych piecach hartowniczych nagrzewanie szkła polega na wymianie promieniowania cieplnego pomiędzy rezystorami a szkłem. Oprócz promieniowania zachodzi tu również konwekcja naturalna i kontaktowe przenoszenie ciepła z walców na szkło. Obecnie takie piece są już rzadko spotykane na rynku, ze względu na wymagania związane z hartowaniem powlekanego szkła niskoemisyjnego.
Powierzchnia szkła z powłoką niskoemisyjną, umieszczoną na górnej powierzchni tafli szkła wkładanej do pieca (aby powłoka nie miała kontaktu z rolkami przesuwającymi się po dolnej powierzchni tafli), może odbijać nawet 96% promieniowania cieplnego emitowanego przez gorące powierzchnie pieca. Zatem ogrzewane takiego szkła przez promieniowanie jest mało skuteczne (szczególnie właśnie górnej powierzchni takiego szkła).
Przy wymuszonej konwekcji można zintensyfikować nagrzewanie powlekanej górnej strony szkła, aby zachować symetryczny profil temperaturowy według grubości, tj. zachowanie płaskich powierzchni szkła w piecu (źle ogrzewane szkło ulega odkształceniom). Konwekcja wymuszona jest prowadzona za pomocą strumieni powietrza, które są skupione i kierowane w szklaną powierzchnię. Konwekcja wymuszona jest używana razem z promieniowaniem, aby zintensyfikować przenoszenie ciepła nawet w przypadku przezroczystego szkła.
Producenci pieców mają jednak odmienne zdanie na temat zdolności konwekcyjnej pieców, które produkują. Niniejszy artykuł ma na celu wyjaśnienie tych kwestii. Przeanalizowano w nim teoretycznie trzy modele pieców, aby opisać zjawiska przenoszenia ciepła wewnątrz tych pieców.
Różne typy pieców do hartowania na rynku
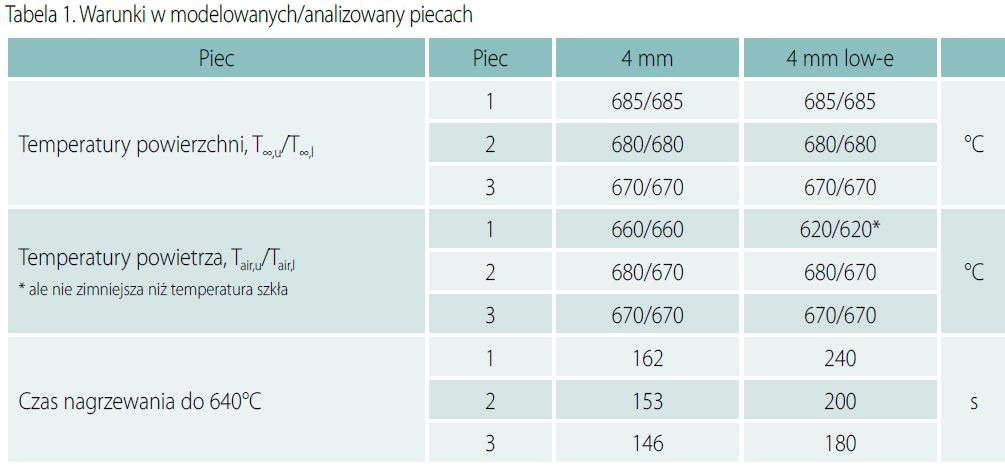
Na rynku dostępna jest szeroka oferta pieców do hartowania, a urządzenia te różnią się sposobem tworzenia, ogniskowania i sterowania promieniowaniem oraz konwekcyjną wymianą ciepła. Dość typowa prędkość nagrzewania dla przezroczystego szkła wynosi 40 s/mm x grubość szkła w mm, która różni się nieznacznie w zależności od grubości szkła i modelu pieca. Czas nagrzewania szkła z powłoką niskoemisyjną jest dłuższy i dużym stopniu zależy od modelu pieca.
Górne grzejniki wewnątrz pieca to zwykle niezakryte spirale, czyli rezystory elektryczne emitujące ciepło bezpośrednio w kierunku szkła (patrz typ A na rysunku 2.1). Grzejniki z otwartymi spiralami umieszczone na dole pieca mają cienkie stalowe osłony chroniące je przed rozbitym szkłem (szkło czasami pęka podczas hartowania). Bezpośrednie promieniowanie z dolnych rezystorów, a dokładniej z pokryw (wspomnianych wcześniej) na szkło jest stosunkowo niskie ze względu na wąskie szczeliny między rolkami. Zatem główna droga przenoszenia ciepła promieniowania do szkła na dolnej stronie polega na tym, że dolne rezystory promieniują na rolki (które zostają w ten sposób nagrzane), a te z kolej po nagrzaniu promieniują na szkło.
Przenoszenie ciepła przez promieniowanie z gorących powierzchni wewnątrz pieca do szkła zależy od właściwości promieniowania tych powierzchni oraz temperatury. Właściwości radiacyjne gorących powierzchni, tj. rezystorów, rolek, ścian i skrzynek z dyszami nie przedstawiają dużych różnic w zależności od modelu pieca, ale ich względna powierzchnia, którą szkło „widzi”, jest odmienna. Jednak różnice w szybkości wymiany ciepła promieniowania w piecach zależą głównie od ustawionej temperatury. Wynikają one także – choć w mniejszym stopniu – od rozmieszczenia termopar mierzących lokalne wartości temperatury pieca, a także od sposobu, w jaki zaprogramowany został system kontrolujący te wartości temperatur.
Typowa zaprogramowana wysokość temperatury w piecu wynosi od 670 do 720°C. Wyższa wartość powoduje nie tylko zwiększoną prędkość ogrzewania, ale też nieuchronnie prowadzi do zróżnicowania lokalnych i średnich wartości temperatury hartowania szkła. Ogrzewanie pozostaje lepiej zbalansowane, gdy te same ustawione temperatury mogą być używane dla grzałek umieszczonych na górnych i dolnych stronach pieca, w ramach zaprogramowanych procedur ogrzewania.
Istnieją dwie różne technologie stosowane do realizacji konwekcji w piecach do hartowania: konwekcja z zasysanym powietrzem zewnętrznym i konwekcja z zamkniętym obiegiem powietrza. W pierwszym przypadku świeże powietrze jest zasysane z zewnątrz pieca i pod ciśnieniem wdmuchiwane w kierunku szyby przez otwory w rurach konwekcyjnych. Konwekcja ta jest również nazywana konwekcją zasysania powietrza lub konwekcją powietrza przepływającego, ponieważ taka sama ilość powietrza wdmuchiwanego do pieca jest również wydmuchiwana z niego. Zwykle powietrze jest sprężane za pomocą sprężarki do 8-12 barów, a nadciśnienia wewnątrz rury konwekcyjnej, tj. ciśnienie nadmuchu, jest ustawiane w zakresie od 0 do 4 barów (w zależności od receptury grzania).
Ciśnienie nadmuchu jest kontrolowane za pomocą zaworów umieszczonych na zewnątrz pieca. Typowa średnica otworu do wydmuchiwania wynosi 1–2 mm, a wewnątrz pieca na powierzchni jednego metra kwadratowego znajduje się 10-80 otworów. Taka konwekcja nazywana jest konwekcją sprężonego powietrza. Może to być nawet jedyny sposób zorganizowania konwekcji powietrza z zewnątrz, ale jest bardzo możliwe, że niektórzy producenci pieców próbują uniknąć wyraźnego naruszenia patentu [2A], używając wentylatorów lub turbowentylatorów zamiast sprężarki (kompresora) do dostarczania świeżego powietrza do otworów nadmuchowych w dolnej części pieca .
W technologii konwekcji z zamkniętym obiegiem powietrze jest zasysane przez wentylatory wewnątrz pieca i kierowane do otworów nadmuchowych oraz wydmuchiwane w kierunku szyby. W ten sposób unikamy dostarczania powietrza z zewnętrz. Szybkość konwekcji jest kontrolowana przez zmianę prędkości obrotowej wirnika wentylatora za pomocą regulatora częstotliwości, który zmienia ciśnienie nadmuchu. W najprostszych systemach konwekcji powietrza obiegowego rury konwekcyjne lub skrzynki z dyszami są umieszczane pomiędzy, nad lub pod rezystorami grzejnymi.
W takiej konstrukcji temperatura powietrza nie jest kontrolowana, a na początku grzania mocno spada w zależności od stopnia obciążenia. Temperatura powietrza jest znacznie bardziej stabilna, gdy rezystory znajdują się w głównym kanale doprowadzającym powietrze (patrz typ B, rysunek1) lub wewnątrz skrzynek z dyszami (typ C, rysunek 1), ponieważ powietrze jest zmuszone do przepływu przez rezystory.
Rezystory umieszczone w kanale doprowadzającym powietrze najpierw przenoszą ciepło głównie do powietrza, a następnie z powietrza do szyby. Taki system z termoparą w głównym kanale doprowadzającym powietrze zapewnia dobrze kontrolowaną temperaturę powietrza, ale promieniowanie skierowane w stronę szyby, pozostaje bez kontroli. W związku z tym temperatura powierzchni promieniujących do szkła silnie spada na początku nagrzewania.
Systemy konwekcji powietrza obiegowego z otwartymi rezystorami spiralnymi wewnątrz skrzynek dysz są często sterowane za pomocą termopar . Są one zamontowane na powierzchni skrzynek z dyszami promieniujących w kierunku szkła, co zapewnia precyzyjną kontrolę wymiany ciepła przez promieniowanie. Temperatura powierzchni obudowy dyszy i termopary spada, gdy w jej zasięgu działania/otoczeniu znajduje się zimne szkło. Następnie włącza się rezystor wewnątrz dyszy i temperatura wkrótce zaczyna rosnąć aż osiągnie ustaloną wcześniej wartość. Rezystor podgrzewa również powietrze uderzające w szybę w zasięgu/polu jego działania.
W związku z tym zarówno promieniowanie, jak i konwekcja są kontrolowane za pomocą tego samego rezystora. W systemie konwekcji powietrza obiegowego (krążącego w obiegu zamkniętym) średnica otworów nadmuchowych wynosi zwykle od 5 do 15 mm, a 100 do 400 otworów znajduje się w na powierzchni jednego metra kwadratowego w piecu, a ciśnienie nadmuchu wynosi od 100 do 1000 Pa.
W szczególności, gdy podgrzewane są szkła z powłoką niskoemisyjną (umieszczoną na górnej powierzchni szkła), transfer ciepła przez konwekcję musi być znacznie wyższy na górnej stronie tafli szkła niż na dolnej. Konwekcja powietrza obiegowego jest zwykle silniejsza niż konwekcja powietrza zewnętrznego (z zasysaniem powietrza z zewnątrz), ale system konwekcji powietrza obiegowego kosztuje znacząco więcej.
Fakt ten uwzględniono w piecach, w których konwekcja powietrza obiegowego prowadzona jest na górnej powierzchni szkła, a konwekcja sprężonego powietrza zewnętrznego na dole [2A]. Takie rozwiązanie jest bliskie optymalnemu, ponieważ konwekcja na dole jest dobrym narzędziem do utrzymywania płaskich tafli szklanych na wczesnych etapach ogrzewania, które często wykonuje się przy dość niskim stopniu konwekcji. Rys. 2.2 przedstawia pozostałe dostępne na rynku kombinacje konwekcji na stronie górnej i dolnej.
Najnowsza kombinacja zawiera konwekcję powietrza obiegowego i zewnętrznego ogrzewająca taflę szkła od góry, a konwekcję powietrza zewnętrznego od spodu. Czasami połączenie konwekcji powietrza obiegowego od góry i od dołu określane jest jako konwekcja pełna, co często daje błędne wrażenie szybkości konwekcji w takim piecu.
Nazewnictwo systemów konwekcyjnych jest dość niekonwencjonalne wśród producentów pieców, mimo że istnieją tylko dwie technologie i kilka ich kombinacji. Z drugiej strony jest to zrozumiałe, ponieważ możliwości różnych systemów konwekcji powietrza obiegowego, a także systemów konwekcji powietrza zewnętrznego są różne. Rysunek 2 pokazuje dostępne kombinacje systemów konwekcyjnych w piecach, w których hartowane jest szkło.
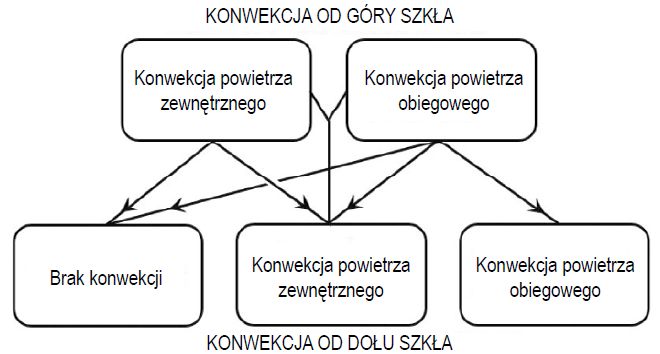
Rys. 2. Dostępne kombinacje konwekcyjne w piecach do hartowania szkła odbicie. Dzięki absorpcji natężenie promieniowania
Zjawiska wymiany ciepła w piecach do hartowania
Promieniowanie cieplne
Na rysunku 3 schematycznie przedstawiono zachowanie promieniowania padającego na płytę szklaną. Na granicy/styku powietrze-szkło odbija się część promieniowania. Współczynnik odbicia ρ zależy od kąta padania i długości fali [1]. Ze względu na niski współczynnik odbicia przezroczystej powierzchni szkła (typowa wartość uśredniona wynosi 0,09), główna część promieniowania przechodzi przez powierzchnię graniczną. Natomiast ta część widma promieniowania, na które szkło jest nieprzezroczyste, jest pochłaniana na powierzchni szkła.
Promieniowanie (dla którego szkło jest przezroczyste) wnika głębiej w szkło, i jest przez nie częściowo pochłaniane. Reszta promieniowania dociera do granicy faz szkło-powietrze, gdzie następuje drugie słabnie, gdy rozchodzi się w szkle. Natężenie promieniowania po drodze x w ośrodku wynosi
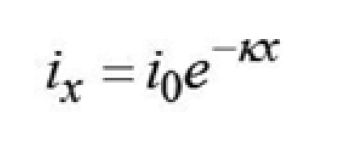 (1)
(1)
gdzie i0 to natężenie na powierzchni, a κ to współczynnik pochłaniania. Szkło sodowo-wapniowe ma dwie graniczne długości fal, przy których jego współczynnik absorpcji ulega zasadniczej zmianie. Praktycznie rzecz biorąc, szkło jest nieprzezroczyste dla promieniowania cieplnego, gdy długość fali przekracza 4,5 μm, podczas gdy dla długości fal poniżej 2,75 μm szkło jest bardzo przezroczyste.
Przy długościach fal od 2,75 do 4,5 μm współczynnik absorpcji wynosi około 4 cm-1, co nadal jest stosunkowo wysoką wartością. Przy długościach fal od 1 do 2,75 μm współczynnik absorpcji wynosi około 0,3 cm-1. Absorpcja widma promieniowania dla przezroczystego szkła o grubości 4 mm wynosi 0,77 (czyli 77% padającego promieniowania) gdy κλ = 4 cm-1 i 0,12 (czyli 12% padającego promieniowania), gdy κλ = 0,3 cm-1. Bezpośrednia absorpcja promieniowania przez „wnętrze „tafli szkła może zmniejszyć szok termiczny w szkle na początku nagrzewania [3]. Powłoka niskoemisyjna na szklanej powierzchni jest jak lustro odbijające promieniowanie (dla promieniowania padającego w piecu do hartowania).
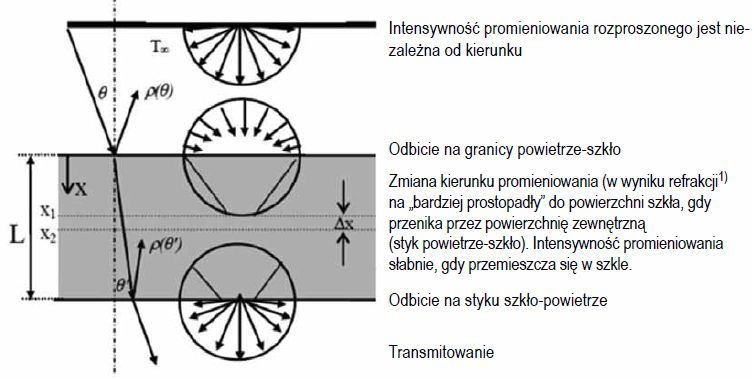
Rys. 3. Zachowanie się padającej wiązki promieniowania w szkle
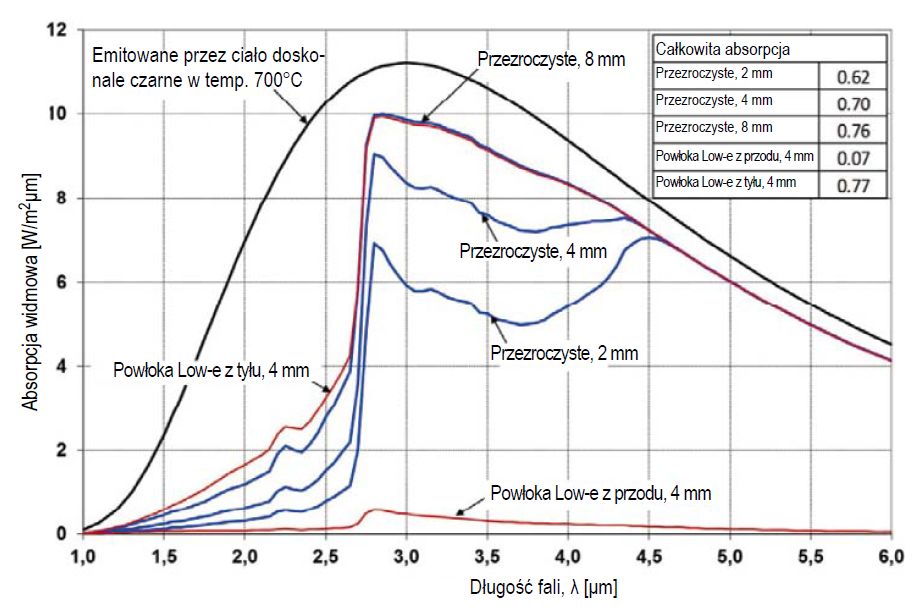
Rys. 4. Absorpcja widmowa w szkle z promieniowania emitowanego przez ciało doskonale czarne w 700°C dla różnych grubości szkła przezroczystego i szkła z powłoką niskoemisyjną (Low-e)
Właściwości radiacyjne niektórych powłok niskoemisyjnych podano ze szczegółami w opracowaniu [1], z której wybrano następujące główne punkty. Powłoka niskoemisyjna selektywnie zmienia współczynnik odbicia na powierzchni szkła (w zależności od długości docierającej fali elektromagnetycznej). Dla światła widzialnego (0,4 <λ <0,7 μm) współczynnik odbicia pozostaje prawie stały, ale przy nieco dłuższych falach współczynnik ten gwałtownie wzrasta do 0,8-0,98, w zależności od rodzaju powłoki. Sama powłoka również pochłania promieniowanie, a absorpcja widmowa nieznacznie wzrasta wraz z temperaturą.
Biorąc pod uwagę kierunkowy współczynnik odbicia widmowego i widmowy współczynnik absorpcji z równania Bouguera2 (3.1), możliwe jest sformułowanie kierunkowej absorpcji widmowej i emitancji (emisyjności) termicznej3 tafli szklanej. W przypadku całkowitych wartości dla półkuli konieczne jest całkowanie po kącie biegunowym 0-90° i widmie długości fali. W metodzie uśrednionego promieniowania netto (Averaged Net Radiation method) opracowanej w [1] dla przezroczystego i powlekanego szkła, skomplikowaną integrację zastąpiono przez zastosowanie specjalnych uśrednionych kierunkowych wartości współczynnika odbicia widmowego i kąta penetracji/ przenikania w płycie szklanej. Całkowanie po długościach fal jest objęte za pomocą pasm długości fal, wewnątrz których właściwości promieniowania są całkowicie niezależne od długości fali.
Rys. 4 i 5 ilustrują metodę opisaną powyżej. Ciało doskonale czarne jest wyidealizowanym ciałem fizycznym, które pochłania całe promieniowanie padające, niezależnie od długości fali lub kąta padania. Ciało czarne jest również idealnym emiterem, a jego emisja wynosi 1. Rysunek 4 przedstawia rozkład widmowy krzywej natężenia emisji promieniowania ciała doskonale czarnego (zgodnie z prawem Stefana- Boltzmanna4) przy T = 700°C, która jest typową temperaturą w piecu do hartowania.
1 Refrakcja – zmiana kierunku rozchodzenia się fali elektromagnetycznej lub akustycznej, załamanie fali związane ze zmianą jej prędkości, gdy przechodzi do innego ośrodka. Zmiana prędkości wiąże się ze zmianą długości fali, podczas gdy częstotliwość pozostaje stała.
2 Prawo Bouguera (zwane również prawem Lamberta) – prawo dotyczące absorpcji (pochłaniania) światła (fali elektromagnetycznej) w ośrodku materialnym. Mówi ono, że natężenie światła przechodzącego przez warstwę substancji maleje wykładniczo wraz ze wzrostem grubości tej warstwy (patrz wzór1).
3 Emitancja termiczna lub emisyjność termiczna to stosunek emitowanego promieniowania cieplnego przez obiekt określonej powierzchni do obiektu idealnie czarnego. Emisyjność termiczna jest wielkością bezwymiarową podaną w zakresie od 0 (ciało doskonale białe) do 1 (ciało doskonale czarne), reprezentującymi względną / porównawczą emisję w odniesieniu do ciała czarnego działającego w podobnych warunkach
4 Prawo Stefana-Boltzmanna – prawo opisujące całkowitą moc wypromieniowywaną przez ciało doskonale czarne w danej temperaturze. Zostało opracowane w 1879 przez Jožefa Stefana i Ludwiga Boltzmanna.
Φ = σ T4,gdzie:
Φ – strumień energii wypromieniowywany z jednostki powierzchni [W/m2],
σ – stała Stefana-Boltzmanna,
T – temperatura w skali Kelvina.
Obszar między krzywą a osią długości fali odpowiada całkowitej „mocy emisyjnej” ciała czarnego σT4 = 51 kW/m2, z czego 46% jest nieprzezroczyste (λ> 4,5 μm) dla szkła. Widmo absorpcji z tej mocy emisyjnej dla przezroczystego i powlekanego szkła niskoemisyjnego o grubości 4 mm pokazano na rysunku 4. Jedna srebrna powłoka znajduje się z przodu lub z tyłu szklanej powierzchni (czyli od strony padania promieniowania i odwrotnie).
Niepowlekana strona szkła z powłoką niskoemisyjną jest bardziej chłonna niż szkło przezroczyste, gdy długość fali jest poniżej nieprzezroczystego pasma. To zjawisko wynika z tego, że promieniowanie, które przenika przez grubość szkła jest głównie odbijane z powrotem od powłoki na jego tylnej powierzchni, a następnie jest ono częściowo absorbowane przez szkło lub bezpośrednio wchłonięte przez powłokę.
Rysunek 4 przedstawia również łączne wartości absorpcji, które dla przezroczystego szkła o grubości 4 mm wynoszą 0,70. Zatem przezroczyste szkło o grubości 4 mm pochłania 70% z 51 kW/m2 (wspomnianych powyżej). Jednak w praktyce nie jest to takie proste, ponieważ powierzchnie wewnątrz pieca do hartowania nie osiągają właściwości ciała doskonale czarnego.
Rozkład widmowy mocy emisyjnej przesuwa się w kierunku krótszych długości fal, gdy wzrasta temperatura szkła. Zatem większa część emisji występuje przy długościach fal, dla których szkło jest przezroczyste. Rysunek 5 przedstawia całkowitą półkulistą emitancję przezroczystego szkła. Przy nieskończonej grubości, a początkowo także przy największych grubościach na rys. 5, emitancja rośnie wraz z temperaturą. Wynika to ze wzrostu współczynnika odbicia powierzchni szkła przy długościach fal powyżej 8 μm.
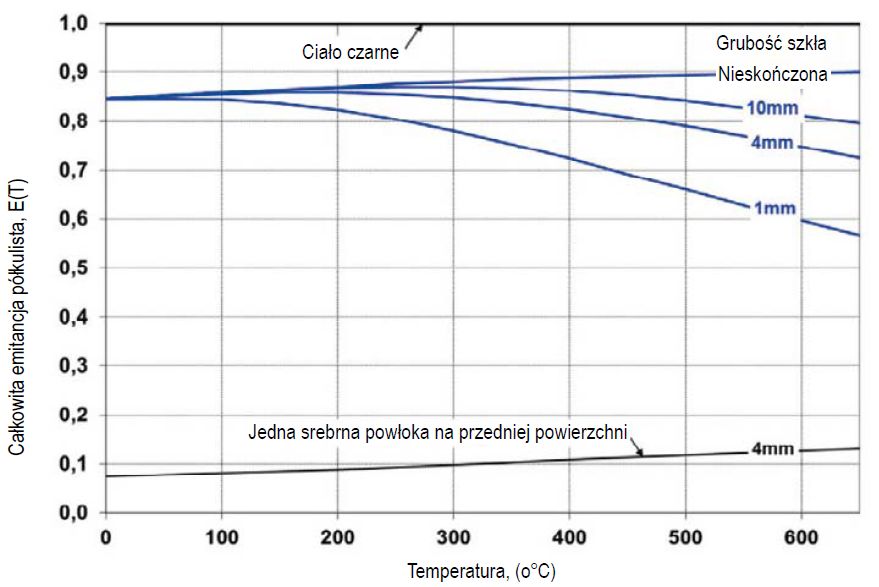
Rys. 5. Całkowita półkulista emitancja przezroczystego szkła sodowo-wapniowego i z powłoką niskoemisyjną
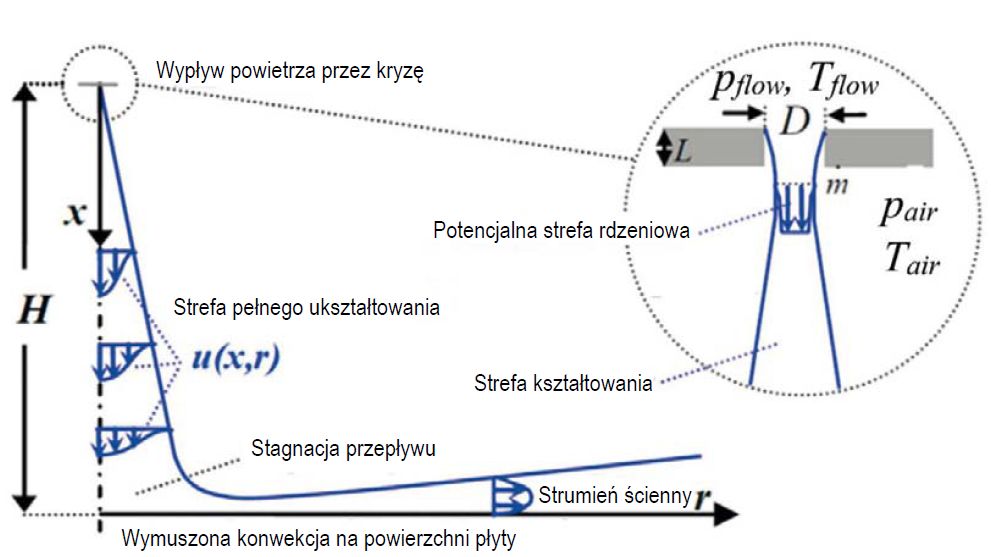
Rys. 6. Szczegóły przepływu strumienia powietrza
Konwekcja wymuszona
Powietrze wypływające z okrągłego otworu tworzy osiowo-symetryczny strumień. Rysunek 6 przedstawia uśrednione w czasie szczegóły przekształcania się turbulentnego strumienia powietrza. Po wypuszczeniu(opuszczeniu dyszy) strumień zaczyna napędzać otaczające powietrze i rozprzestrzenia się, zmniejszając prędkość i zwiększając masowy przepływ. W piecu do hartowania, ze względu na stosunkowo duże odległości nadmuchu (od wylotu dyszy do powierzchni szkła), temperatura strumienia napływającego na płytę szklaną jest znacznie bardziej zależna od temperatury otaczającego powietrza Tair niż początkowa temperatura wypływającego strumienia Tflow.
Transfer ciepła z pojedynczego strumienia powietrza na powierzchnię szkła zależy od ciśnienia nadmuchu (pflow-pair), średnicy otworu (kryzy/ zwężki) D, rodzaju dyszy, odległości między kryzą a szkłem H, kąta padania strumienia na powierzchnię odbierającą ciepło oraz od termicznych właściwości powietrza. Oprócz wyżej wymienionych czynników wpływających na transfer/ przenoszenie ciepła przez układy strumieni powietrza w piecu do hartowania, wymienić też trzeba liczbę otworów nadmuchowych w danym obszarze i odległości między nimi.
Współczynniki przenikania ciepła dla różnych układów strumieni można rozwiązać za pomocą modelowania numerycznego (Computational Fluid Dynamics CFD5), eksperymentalnie lub na podstawie korelacji podanych w literaturze. Rysunek 7 przedstawia przykład zmierzonych lokalnych współczynników przenikania ciepła na powierzchni szkła ogrzewanym strumieniem powietrza typowym dla konwekcji sprężonego powietrza. Na rysunku lokalny współczynnik przenikania ciepła w pobliżu punktu stagnacji silnie rośnie, gdy zmniejsza się odległość nadmuchu H.
Gdy odległość od punktu wypływu strumienia powietrza do punktu stagnacji wzrasta, wpływ H na lokalny przepływ ciepła zanika. Wysoki współczynnik konwekcji lokalnej w punktach stagnacji powoduje powstanie gorętszych pasm na szkle, jeśli odległość nadmuchu jest zbyt mała w stosunku do odległości między otworami nadmuchowymi w piecu do hartowania.
Ocena prawidłowej wartości średniego współczynnika transferu ciepła przez konwekcję h jest często trudna, ale za jego pomocą można łatwo określić konwekcyjny strumień ciepła oraz różnicę temperatur powietrza i powierzchni szkła qc = h (Tair -Tsurface).
5 Obliczeniowa dynamika płynów (CFD) to gałąź mechaniki płynów, która wykorzystuje analizę numeryczną i struktury danych do analizowania i rozwiązywania problemów związanych z przepływami płynów . Komputery służą do wykonywania obliczeń wymaganych do symulacji swobodnego przepływu płynu oraz interakcji płynu (cieczy i gazów) z powierzchniami określonymi przez warunki brzegowe.
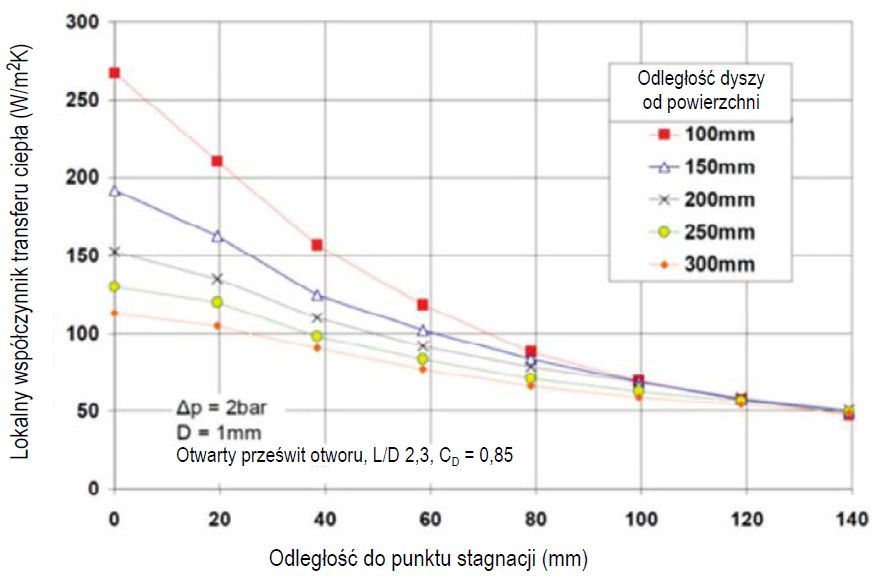
Rys. 7. Eksperymentalne lokalne współczynniki transferu ciepła przedstawione dla różnych odległości dyszy od powierzchni
Kontaktowa wymiana ciepła
Dolna powierzchnia szkła i prowadnice rolkowe (walce ceramiczne służące do przesuwania szkła w piecu) mają linię styku zależną od odległości między rolkami, która zwykle wynosi od 100 do 150 mm (przy gęściej ułożonych walcach jest więcej linii styku). Przenikanie ciepła w miejscu styku to przewodnictwo stałe punktowe między walcem a szkłem. Poza obszarem styku działa przewodzenie przez bardzo cienką szczelinę powietrzną. Kontaktowe przenoszenie ciepła między walcem a punktem na dolnej powierzchni szkła następuje tylko w krótkim czasie kontaktu tct = lct/u.
Następnie kontaktowy impuls przenikania ciepła rozpoczyna się po czasie (Lrp-lct)/u, gdy punkt na dolnej powierzchni szkła styka się z następnym wałkiem. Efektywny współczynnik przenikania ciepła przez kontakt hct to średnia wartość w okresie czasu Lrp/u, a parametry: lct to długość kontaktu, Lrp to skok rolek, a u prędkość szkła.
Strumień ciepła qct z kontaktowym przenoszeniem ciepła do szkła jest iloczynem efektywnego współczynnika kontaktowego przenikania ciepła i różnicy temperatur pomiędzy powierzchnią walca a powierzchnią dolną szkła. W [1] podano, że efektywny współczynnik kontaktowego przenikania ciepła między szkłem a walcami w piecu do odpuszczania wynosi 1 ≤ hctLrp ≤ 3 W/(mK). Jest to wprawdzie dość duży zakres, ale w praktyce bardzo trudny do ograniczenia do poziomu dokładniejszych wartości. Kontaktowe przenoszenie ciepła z rolek na szkło jest zjawiskiem spontanicznym, którego nie można kontrolować podczas ogrzewania i które nie ma dużej zmienności zależnej od typu pieca.
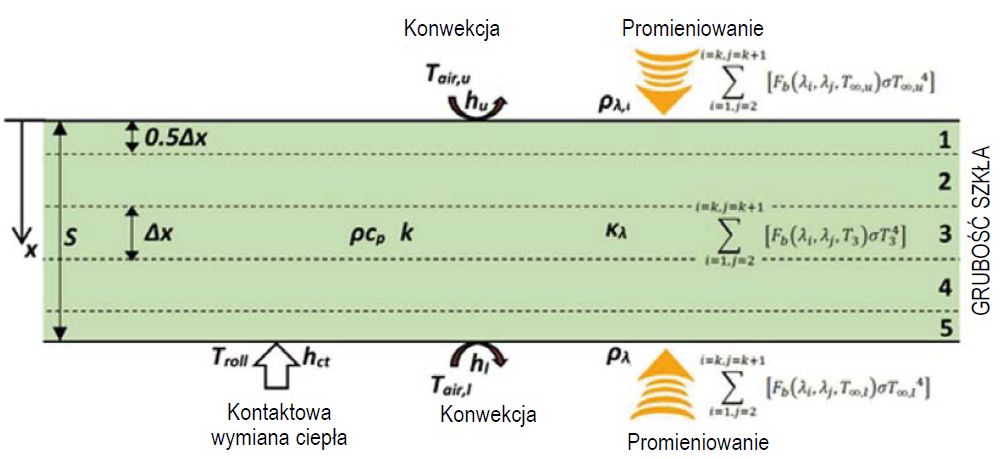
Rys. 8. Jednowymiarowy model obliczeniowy nagrzewania płyty szklanej przez promieniowanie, konwekcję i kontaktowe przenoszenie ciepła
(...)
(...)
dr Mikko Rantala, Glaston
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. Tampere w Finlandii
Bibliografia
[1] Rantala, M., Zjawiska wymiany ciepła w procesach obróbki cieplnej szkła float (Heat Transfer Phenomena in Float Glass Heat Treatment Processes). Tampere Universityof Technology. Publication, Vuosikerta. 1355,Tampere University of Technology, 2015.
[2] Patents: A=EP1491509, B=EP1737800,C=EP2433912.
[3] Karvinen, R. Rantala, M., Transfer ciepła w piecu do hartowania (Heat Transfer in Tempering Furnace). GPD 1999, Tampere- Finland, p. 52-55.

Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 2/2021









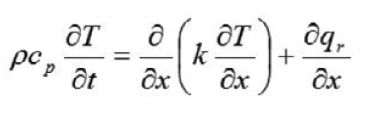 (2)
(2)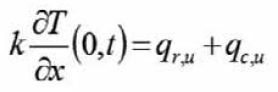 (3)
(3)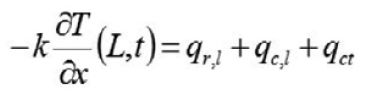 (4)
(4)