W ostatnich latach wśród klientów i producentów pojawiły się spory dotyczące anizotropii (dwójłomności wywołanej naprężeniami wewnętrznymi, która może powodować widoczne przebarwienia w szkle) w przypadku produktów szklanych, takich jak szkło wzmacniane termicznie (HS heat-strengthened) lub całkowicie hartowane (FT fully tempered). Wyniki ostatnich badań pokazują, że anizotropię należy oceniać w różnych aspektach.

Rys. 1. Fasada z szybami ze szkła hartowanego, po lewej silna anizotropia, po prawej niska anizotropia, bez użycia filtrów polaryzacyjnych (Luksemburg)
Ponadto obowiązkowe jest oszacowanie/klasyfikowanie anizotropii przy użyciu odpowiedniej metody oceny. W niniejszym artykule Uniwersytet RWTH w Aachen (RWTH) i Uniwersytet Techniczny w Monachium (HSM) przedstawiają dwie nieniszczące metody, oparte na fotoelastyczności1, do oceny całej powierzchni tafli szklanej.
W szczególności wykazano, że obie metody są odpowiednie do obiektywnej oceny anizotropii. Najpierw zademonstrowano metodę wyznaczania naprężeń w rejonie brzegowym/krawędziowym, a następnie wizualizację i badanie anizotropii w obszarze wewnątrz szyby.
1. Wstęp
W trakcie produkcji wyrobów szklanych z wprowadzonymi w procesie obróbki termicznej naprężeniami wewnętrznymi – może wystąpić niejednorodny rozkład naprężeń na powierzchni tafli szkła wskutek nierównomiernego chłodzenia.
Jeżeli naprężenie wstępne we wszystkich kierunkach jest nierównomierne, efektem dwójłomności2 jest widoczne zjawisko opalizacji, które często można zaobserwować jako szare lub kolorowe paski lub plamki na powierzchni szyby (por. rys. 1).
Zjawisko to jest również określane jako anizotropia. Jednak w normach dotyczących szkła [1] i [2] anizotropia nie jest scharakteryzowana jako wada, ale jako cecha fizyczna hartowanego termicznie szkła.
Intensywność anizotropii zależy od niejednorodności naprężeń wstępnych (wywołanych obróbką termiczną): im większa anizotropia, tym więcej opalizacji/iryzacji3 (iridescence) może się pojawić [4].
W przypadku występowania (częściowo) spolaryzowanego światła anizotropia może być optycznie wykryta. Im wyższy stopień polaryzacji, tym lepiej można wykryć opalizację [5].
Światło spolaryzowane jest częścią środowiska naturalnego i powstaje w wyniku rozpraszania i odbicia. Stopień polaryzacji światła zależy od kilku parametrów, takich jak pozycja słońca na widnokręgu czy kąt odbicia od szklanej fasady.
W omawianym projekcie badawczym celem badań jest ocena jakości szkła według podstawowych wymagań, takich jak wytrzymałość, spękanie i właściwości optyczne – przeprowadzana w sposób nieniszczący.
Projekt badawczy obejmuje również opracowanie algorytmu oceny do obliczania anizotropii oraz metody pomiarowej do wyznaczania naprężeń obszarze brzegowym/krawędziowym tafli.
Jedną z dużych zalet tej metody jest ocena anizotropii występującej na powierzchni wewnątrz obszaru tafli szkła poprzez wykluczenie nieuniknionych anizotropii indukowanych geometrycznie, takich jak krawędzie, narożniki lub otwory/wydrążania (por. rysunek 2).

Rys. 2. Przykłady anizotropii wywołanych/indukowanych geometrią: krawędź, narożnik i otwór
1 Fotoelastyczność – występowanie lub zmiana dwójłomności pod wpływem naprężenia. Zjawisko to jest powszechnie stosowane do określania i wizualizacji rozkładu naprężeń w badanym materiale, zwłaszcza przy skomplikowanych lub nieregularnych kształtach, jak również w modulatorach akustyczno-optycznych.
2 Dwójłomność – zdolność ośrodków optycznych do podwójnego załamywania światła (rozdwojenia promienia świetlnego). Zjawisko to wynika z faktu, że substancja jest anizotropowa, co oznacza, że współczynniki przenikalności elektrycznej ε i wynikająca z niego prędkość światła, a co za tym idzie współczynnik załamania światła, w krysztale zależy od kierunku drgań pola elektrycznego fali elektromagnetycznej (polaryzacji fali).
3 Opalizacja, iryzacja to zjawisko widoczne na niektórych powierzchniach, które wydają się stopniowo zmieniać kolor wraz ze zmianą kąta widzenia lub kąta oświetlenia. Jest to często spowodowane wielokrotnymi odbiciami od dwóch lub więcej półprzezroczystych powierzchni, w których przesunięcie fazowe i interferencja odbić modulują światło padające (wzmacniając lub tłumiąc niektóre częstotliwości bardziej niż inne).
W niniejszym artykule, w pierwszej kolejności, omówiono fizyczne podstawy anizotropii. Następnie przedstawiono metodę pomiarową do dwuwymiarowej detekcji/wykrywania i opisu anizotropii w termicznie hartowanych taflach szklanych, porównano ją z istniejącą już metodą analizy, a na koniec zaprezentowano pierwsze wynik
Jedną z metod badania anizotropii w szkle hartowanym termicznie jest zastosowanie tzw. polaryskopów. W ramach przeprowadzonych badań wykorzystano polaryskop kołowy.
Światło spolaryzowane kołowo nie ma stałego kierunku drgań/ oscylacji i dlatego jest niezależne od kierunku. Zestaw zastosowanego polaryskopu kołowego zawiera dwa polaryzatory i dwie tzw. płyty ćwierćfalowe4, które zawierają materiał dwójłomny. Pierwsza płytka ćwierćfalowa umieszczona jest bezpośrednio za polaryzatorem, druga przed analizatorem.
Polaryzator wytwarza światło spolaryzowane liniowo, które po przejściu przez pierwszą płytkę ćwierćfalową ulega polaryzacji kołowej. Po wejściu do próbki dwójłomnej (np. szkło hartowane) wektor światła jest rozkładany na dwie składowe w zależności od kierunków naprężeń głównych.
Po wyjściu z próbki można wykryć retardację/ opóźnienie s (jak pokazano na rysunku 3). Światło spolaryzowane kołowo jest ponownie polaryzowane liniowo przez drugą płytę ćwierćfalową i ostatecznie przechodzi przez analizator [6].
Otrzymane opóźnienie s zależy od wartości różnic naprężeń głównych w danym punkcie. Różnica naprężeń i opóźnienie są powiązane grubością próbki
d i tak zwaną stałą fotoelastyczną C.
s = C · (σ1 – σ2) ∙ d (1)
Jeżeli dodatkowo różnicę dróg odniesiemy do długości fali (s/λ), to otrzymamy przesunięcie fazowe δ, co daje tzw. główne równanie fotoelastyczności:
δ = (C / λ) · (σ1 – σ2) ∙ d (2)
Jeżeli materiał dwójłomny, np. szkło hartowane, jest oglądany w polaryskopie (aparacie polaryzacyjnym) w świetle monochromatycznym, to na skutek interferencji powstają czarne linie.
Te czarne linie nazywane są izochromatami rzędu 0, 1, 2 itd. w zależności od wielkości przesunięcia fazowego. Izochromaty wskazują punkty w badanej próbce, które mają taką samą różnicę naprężeń głównych σ1 – σ2.
W przypadku stosowania światła białego (mieszanina złożona ze światła o różnych długościach fal) efekty te występują oddzielnie dla każdej długości fali. Wygaszone zostaje tylko światło o określonej długości fali, a izochromaty pojawiają się w barwie dopełniającej do wygaszonego światła (o określonej długości fali) [6].
2.2 Właściwości brzegowe/krawędziowe
Tafle hartowanego szkła płaskiego można podzielić na cztery strefy ze względu na rozkład naprężeń [7]. Powierzchnia płyty z zachowaniem odpowiedniej odległości od krawędzi i otworów tworzy strefę 1.
Naprężenie wstępne σ1 = σ2 w tym obszarze jest odzwierciedlone przez profil paraboliczny na grubości. Przy zbliżaniu się do krawędzi płyty (strefa 2), σ1 prostopadłe do krawędzi przyjmuje wartość zero, jak pokazano na rysunku 4.
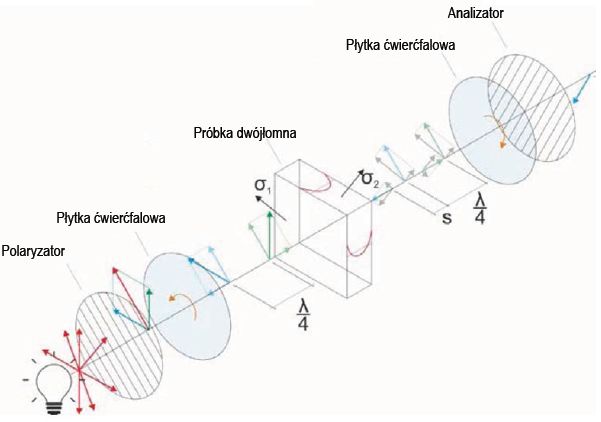
Rys. 3. Funkcjonalność polaryskopu kołowego
Efekt ten prowadzi do tego, że za pomocą różnych metod naprężeniowo-optycznych (stress-optical methods) można wyznaczyć średnie naprężenie ściskające σ2 (naprężenie brzegowe tafli), ponieważ druga niewiadoma σ1 może być pominięta w głównym równaniu naprężeniowo-optycznym.
3. Analityczne metody oceny
Uniwersytety RWTH i HSM niezależnie od siebie opracowały różne metody analizy w celu określenia różnic naprężeń w płaszczyźnie szkła – w celu obiektywnej oceny badanych anizotropii.
Ponadto przedstawiono metodę pomiarową Uniwersytetu HSM do badania krawędziowych naprężeń ściskających w tafli szkła hartowanego termicznie (występujących w brzegowej strefie tafli) za pomocą cyfrowych obrazów z filtra polaryzacyjnego.
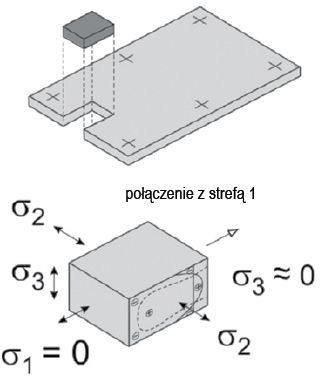
Rys. 4. Rozkład naprężeń w pobliżu krawędzi (strefa 2)
3.1 Metoda HS M
Opisane tu metody analizy opierają się na zasadach wyznaczania porządku izochromatycznego (isochromatic order) na podstawie obrazów z filtrów polaryzacyjnych za pomocą algorytmów komputerowych, jak opisano w [8]. W pierwszej kolejności wyjaśniono metodę wyznaczania średniego naprężenia na brzegu/krawędzi tafli szkła.
Dobrze znaną metodą, którą można również znaleźć w [6], jest wyznaczenie naprężenia σ2 na swobodnej krawędzi elementu poprzez proste obliczenie porządku izochromatycznego. Zastosowana metoda wymaga monochromatycznego źródła światła lub podziału obrazu cyfrowego (światło białe) na trzy kanały barwne: czerwony, zielony i niebieski (RGB red, green and blue).
Wyznaczenie porządku/rzędu izochromatycznego rozpoczyna się zawsze od miejsc wolnych od obciążeń lub izotropowych. W polaryskopie kołowym w połączeniu ze światłem białym plamy te są ciemne (w przeciwieństwie do kolorowych izochromatów wyższego rzędu).
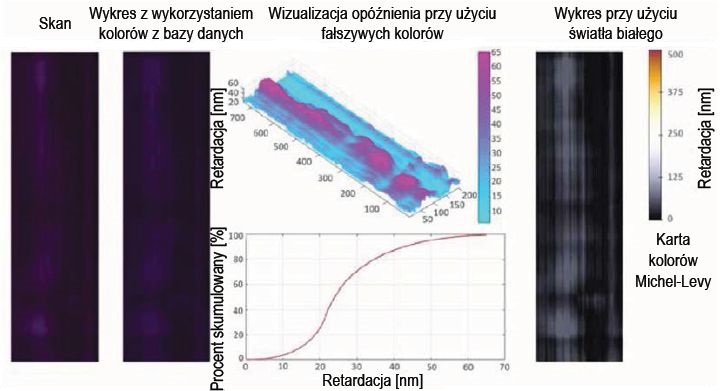
Aby precyzyjnie określić naprężenie brzegowe tafli σ2, musi być znana długość fali światła. Do badań laboratoryjnych użyto soczewkę telecentryczną5 w połączeniu ze źródłem światła białego, aby uzyskać obrazy z filtrów polaryzacyjnych (por. rys. 5), z których można odczytać położenie izochromatów.
Mając rząd n i znaną długość fali λ użytego światła, dla każdego izochromatu wyznaczana jest związana z nim retardacja przez pomnożenie rzędu przez długość fali.
Ponieważ maksimum i minimum jasności zmieniają się o pół rzędu, kolejny punkt można znaleźć pomiędzy dwoma izochromatami. Opóźnienie/retardancję s wyznacza się przez ekstrapolację punktów pomocniczych/podparcia, jak pokazano na rysunku 5.
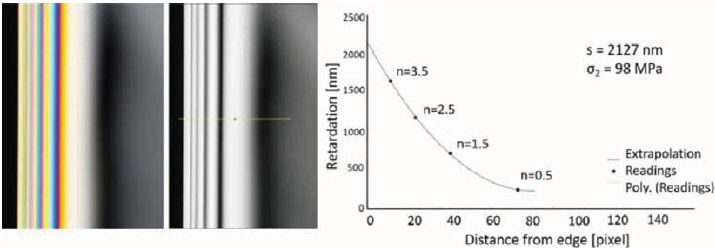
Rys. 5. Obraz z filtrem polaryzacyjnym RGB (po lewej) i monochromatyczny (w środku), wyznaczenie opóźnienia/retardacji s (po prawej)
Korzystając z głównego równania fotoelastyczności i wiedząc, że naprężenie główne σ1 na krawędzi jest równe zeru, brzegowe naprężenie σ2 można uzyskać jako iloraz opóźnienia/retardancji s i iloczynu grubości szkła d i stałej fotoelastycznej C.
Druga metoda analizy, która po raz pierwszy została przetestowana w HSM w 2014 roku, może być wykorzystana do wyznaczenia różnicy dróg na powierzchni szkła dla każdego piksela [3]. Cyfrowa ocena obrazów izochromatycznych jest podstawą do wyznaczenia kwantyfikowalnej, obiektywnej miary dla anizotropii w szkłach hartowanych termicznie.
Sekwencja metody pomiarowej, jak pokazano na rysunku 6, rozpoczyna się od rejestracji obrazów z cyfrowego filtra polaryzacyjnego w ciemnym polu polaryskopu kołowego. W celu uzyskania korelacji pomiędzy barwą światła a różnicą dróg, obowiązkowa jest kalibracja użytej kamery, polaryzatora i źródła światła. Procedura kalibracji została szczegółowo opisana w [8] i opiera się na zaimplementowaniu kompensatora Babinet-Soleil6 do toru wiązki.
W ten sposób można przypisać różnice ścieżek/ dróg do intensywności RGB z przyrostem o 10 nm, które następnie można podzielić na przyrosty o 1 nm za pomocą dalszych obliczeń. Przy użyciu skalibrowanego obrazu filtra polaryzacyjnego można uzyskać różnicę drogi dla każdego piksela za pomocą oprogramowania do analizy.
Algorytm porównuje kolor każdego piksela obrazu z kolorem bazy kalibracyjnej; najlepsze dopasowanie jest obliczane przy użyciu sumy błędów [3] [8].
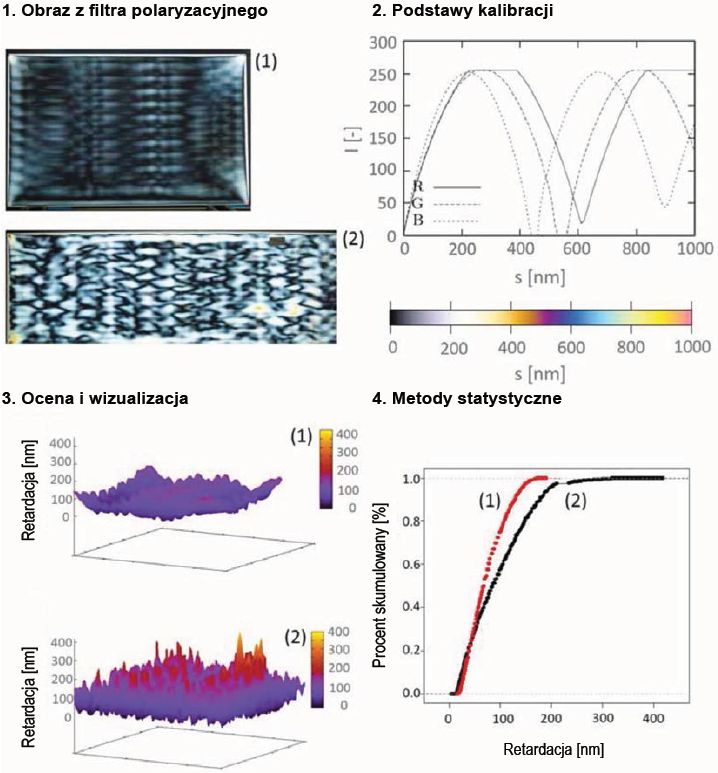
Wyniki analizy obrazu mogą być przedstawione w postaci trójwymiarowych wykresów. Dalsze stochastyczne metody oceny oferują możliwe narzędzie do oceny anizotropii.
Rys. 6. Kolejność prac/czynności w metodzie stosowanej w HSM
5 Telecentryczność – właściwość układu optycznego (na przykład obiektywu fotograficznego) polegająca na wzajemnej równoległości promieni świetlnych z niego wychodzących. Jeśli promienie te padają następnie na materiał światłoczuły (błonę fotograficzną, matrycę), czynią to pod jednakowym kątem (zwykle prostym), co zapobiega zniekształceniom obrazu i jego zaciemnieniom w rogach kadru.
6 Kompensator Babinet-Soleil jest bezstopniowym zwalniaczem zerowego rzędu . Składa się z dwóch klinów dwójłomnych, z których jeden jest ruchomy, a drugi jest przymocowany do płyty kompensacyjnej.
3.2 Metoda RWTH
Metoda analityczna opracowana przez RWTH jest rozwiązaniem z użyciem bazy danych dla dwuwymiarowej analizy anizotropii w szkle hartowanym. W pierwszej kolejności rejestrowane są obrazy z filtra polaryzacyjnego w ciemnym polu w układzie fizycznym przedstawionym na rysunku 3, w celu uzyskania informacji o stanie rozkładu naprężeń wstępnych.
Następnie mierzy się istniejące widmo barwne, zaznacza na wygenerowanych obrazach z filtrów polaryzacyjnych oraz na szybie punkty wyróżniające się kolorystycznie (por. rys. 7) i określa lokalnie naprężenia wstępne wzdłuż kierunków naprężeń głównych (σ1 i σ2) [7] za pomocą programu SCALP-04 firmy Glass Stress Ltd. (patrz rys. 7).
Rys. 7. Rozkład wartości dla koloru czerwonego na tafli szklanej
Ponieważ kierunki naprężeń głównych w próbce mogą się różnić w obrębie badanych próbek, konieczne jest ich wcześniejsze wyznaczenie.
Pomiary przeprowadzane są na tafli szkła zarówno od strony powietrznej jak i od strony cynowej, a następnie łączone są w jedną krzywą. Na podstawie otrzymanej paraboli obliczane są całki naprężeń głównych i odpowiadające im opóźnienia z wykorzystaniem równania głównego fotoelastyczności.
Następnie do każdego punktu i związanego z nim opóźnienia, które wynika z lokalnego pomiaru, przypisywany jest odpowiedni kolor na obrazie z filtra polaryzacyjnego. Wyznaczone punkty danych służą jako punkty pomocnicze przy generowaniu bazy danych. Opracowano algorytm analizujący całą powierzchnię tafli szklanych pod kątem anizotropii.
Algorytm analizuje każdy piksel obrazu z filtra polaryzacyjnego pod względem jego koloru i przypisuje mu odpowiednie opóźnienie/retardację, korzystając z wcześniej wygenerowanej bazy danych. W celu wizualnego porównania i kontroli generowany jest wykres z kolorami bazy danych.
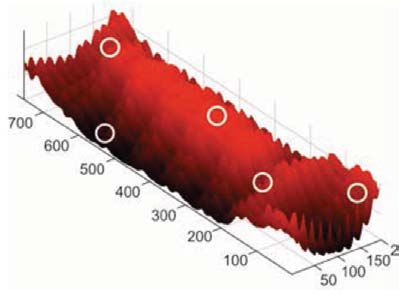
Rys. 8. Wynik/Dane wyjściowe z algorytmu oceny
Anizotropię w obrębie środkowej powierzchni tafli szkła przedstawiono na trójwymiarowym wykresie 3D rozkładu opóźnienia w fałszywych kolorach, jak pokazano na rysunku 8, w celu wyróżnienia obszarów o wysokiej anizotropii ze względu na różnice w kolorze i składowej wysokości. Ponieważ do generowania obrazów z filtrów polaryzacyjnych niekoniecznie jest wymagane użycie światła białego, wykres symuluje obraz wirtualnego z filtra polaryzacyjnego w świetle białym zgodnie z kartą kolorów Michel-Lévy [10].
Pierwszym krokiem w kierunku obiektywnej oceny szkła hartowanego termicznie jest wykrycie rozkładu anizotropii na powierzchni. W tym celu program oblicza skumulowany procent rozkładu opóźnienia i przedstawia go w postaci wykresu. Należy również wspomnieć, że obiektywna ocena jest możliwa tylko wtedy, gdy znane są warunki bazowe w kontekście wykrywania anizotropii.
Rys. 9. Porównanie dwóch metod oceny
3.3 Porównanie
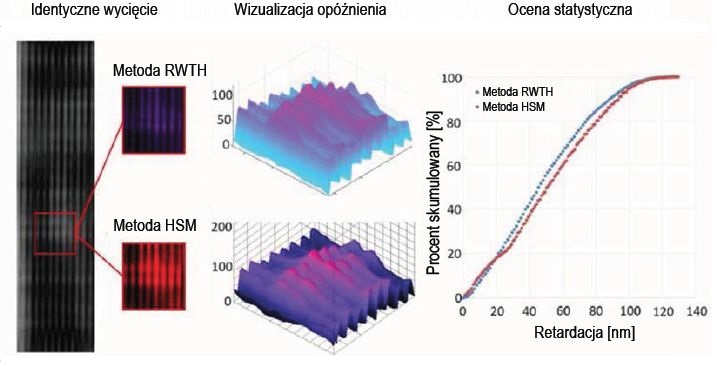
W celu porównania obu metod analizy całej powierzchni tafli szkła przedstawiono przykład badania tego samego fragmentu obrazu szyby termicznie hartowanej z filtra polaryzacyjnego. Ocena została przeprowadzona w odniesieniu do rozkładu i wielkości opóźnień w skumulowanym procencie.
Na rysunku 9 widać, że dwa wykresy powierzchniowe mają bardzo podobny kształt i strukturę. Jasne plamy w obrazie z filtra polaryzacyjnego wskazują na większe opóźnienie/retardację niż ciemne plamy, co jest prawidłowo odwzorowane w ocenie obu metod i skutkuje falistą powierzchnią wykresów 3D.
Przy maksymalnej wartości 129,0 nm, określonej metodą HSM w porównaniu z maksymalnym opóźnieniem/ retardacją wyznaczonym metodą RWTH wynoszącym 126,5 nm, wartości szczytowe obu metod są bardzo zbliżone do siebie (odchylenie 0,98%).
Odchylenia mogą wynikać z niedokładności pomiaru i kalibracji obu metod. Ponadto skumulowane krzywe procentowe wynikające ze względnego rozkładu częstotliwości są bardzo do siebie zbliżone dla obu metod, zwłaszcza w odniesieniu do gradientów/nachylenia krzywych. Ogólnie rzecz biorąc, można zauważyć, że analizowane wartości szczytowe wykazują dobrą zgodność.
4. Wnioski i podsumowanie
W ramach tego artykułu opisano i porównano dwie niezależnie opracowane analizy do wykrywania anizotropii na całej powierzchni wyrobów ze szkła hartowanego termicznie. Ponadto przedstawiono metodę wyznaczania naprężeń w obszarze brzegowym. Stwierdzono, że obie metody analizy anizotropii wykazują dobrą zgodność w zakresie wyników pomiarów.
W tym przypadku przedstawiona ocena statystyczna może być podstawą do ewentualnej oceny anizotropii. Jednak ogólne kryterium oceny nie zostało jeszcze zdefiniowane, ale kryteria oceny anizotropii są obecnie opracowywane przez przemysł szklarski.
Aby móc zintegrować uzyskane wyniki do wykrywania anizotropii w procesie produkcji wyrobów ze szkła hartowanego termicznie, celem projektu badawczego realizowanego przez SoftSolution GmbH i VitroDUR GmbH jest opracowanie procedury on-line do zapewnienia jakości, we współpracy z RWTH i HSM. Zarówno jakość rozkładu naprężeń na powierzchni szkła, jak i stopień „sprężenia” (występowania naprężeń wstępnych) powinny być wiarygodnie określone i udokumentowane.
Niniejsza praca została opracowana w ramach projektu badawczego „Gläsernes Glas” finansowanego przez niemieckie Federalne Ministerstwo Gospodarki i Energii (ZF4053101GM5 i ZF4051701GM5) w ramach Centralnego Programu Innowacji „Mittelstand” (ZIM). Autorzy pragną podziękować wszystkim partnerom projektu za dobrą współpracę.
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. Tampere w Finlandii
Benjamin Schaaf, Pietro Di Biase, Markus Feldmann, Christian Schuler, Steffen Dix
Bibliografia
[1] EN 12150: Szkło w budynkach – Termicznie hartowane bezpieczne szkło sodowo-wapniowo-krzemianowe
[2] EN 1863: Szkło w budynkach - Termicznie wzmocnione szkło sodowo-wapniowo-krzemianowe
[3] Illguth, M.; Schuler, C.; Bucak, Ö.: Wpływ anizotropii optycznej na szklane fasady budynków i metody pomiaru (The effect of optical anisotropies on building glass façades and its measurement methods). Frontiers of Architectural Research, DOI 10.1016/j. foar.2015.01.004, 2015.
[4] Bucak, Ö.; Feldmann, M. et al.: Powtarzalna i weryfikowalna controla jakości, wzrost efektywności giętego szkła termicznie hartowanego (Reproduzierbare und prüfbare Erhöhung der Qualität und damit der Leistungsfähigkeit thermisch vorgespannter gebogener Gläser). Raport końcowy ZIM, 2010 (niepublikowany).
[5] Feldmann, M.; Kasper, R.; Di Biase, P.; Kremens, T.; Bucak, Ö.; Illguth, M.; Wahlers, L.; Reckow, J.; Kubiak, R.: Kontrola jakości ESG i TVG – zastosowanie elastooptyki (Qualitätskontrolle von ESG und TVG – Einsatz der Spannungsoptik). W: Der Stahlbau, Issue 3/12, Ernst und Sohn, DOI 10.1002/stab.201201533, 2012.
[6] Föppl, L.; Mönch, E.: Praktyczna elastooptyka (Praktische Spannungsoptik). Springer-Verlag Berlin, wydanie 3, ISBN 978-3-540-05534-1, 1972.
[7] Feldmann M.; Kasper, R.; Langosch, K.: Szkło na elementy nośne (Glas für tragende Bauteile). Werner Verlag, ISBN 978-3-8041-1626-9, 2012.
[8] Ramesh, K.: Cyfrowa fotoelastyczność: zaawansowane techniki i zastosowania (Digital Photoelasticity: Advanced Techniques and Applications). Springer Verlag, Berlin i Nowy Jork, ISBN 978-3-54066-795-7, 2000.
[9] Feldmann, M.; Schuler, C. et al: Metody wykrywania i analizy anizotropii w wyrobach ze szkła hartowanego termicznie (Methoden zur Erfassung und Analyse von Anisotropien bei thermisch vorgespannten Glasprodukten). Konstruktiver Ingenieurbau. Bundesanzeiger Verlag GmbH Kolonia, 01/2017
[10] Sörensen, B.: Zmieniony wykres Michel-Lévy barw interferencyjnych oparty na obliczeniach (A revised Michel-Lévy interference colour chart based on first- principles calculations), 2012. [1] EN 12150:
































