Wiele materiałów stosowanych w nowoczesnej inżynierii lądowej, takich jak powlekane siatki wzmacniające z włókien węglowych lub międzywarstwy PVB do szkła laminowanego (bezpiecznego), jest produkowanych na bazie polimerów. Materiały polimerowe wykazują typowe zachowanie lepkosprężyste (zależne od czasu lub prędkości odkształcania) oraz zależne od temperatury.

Ponadto, materiały polimerowe mogą wymagać równań konstytutywnych uwzględniających hiperelastyczność (nieliniową relację naprężenie-odkształcenie w warunkach quasi-statycznych) podczas poddawania ich dużym odkształceniom. W kontekście teorii hiperelastyczności, relacje naprężenie-odkształcenie są wyprowadzane na podstawie funkcji swobodnej energii Helmholtza1.

Aby zbadać konstytutywne zachowanie hipersprężyste polimeru przy dużych odkształceniach, można wykorzystać różne metody badań, takie jak test rozciągania jednoosiowego lub dwuosiowego oraz test czystego ścinania (naprężenia normalne są wówczas równe zero) w celu oceny geometrii powierzchni energii swobodnej Helmholtza w płaszczyźnie inwariantów/niezmienników.

W ramach projektu badawczego opisanego w niniejszym artykule przeprowadzono testy rozciągania jednoosiowego i dwuosiowego oraz czystego ścinania na akustycznej warstwie pośredniej PVB w celu oceny odpowiedniej funkcji naprężenie – odkształcenie.

Badanie powierzchni energii swobodnej Helmholtza na podstawie wyników eksperymentalnych pozwala na ocenę właściwego podejścia do energii swobodnej Helmholtza w porównaniu z powszechnie stosowanymi formułami/wzorami matematycznymi, takimi jak modele materiałowe Neo-Hook czy Mooney-Rivlin.

1. Wstęp, stan obecnej wiedzy
Szkło laminowane w stanie nieuszkodzonym zachowuje się liniowo-lepkosprężyście, dzięki czemu międzywarstwa nie ulega dużym odkształceniom. Zachowanie liniowo-lepkosprężyste zostało już omówione w wielu publikacjach np. [1] - [3] i dlatego nie jest tematem niniejszego opracowania.

Jeśli chodzi o zachowanie szkła laminowanego po pęknięciu, to warstwa pośrednia (folia laminująca) ulega dużym odkształceniom i dlatego charakteryzuje się nieliniowym stosunkiem/relacją naprężeń do odkształceń, tzw. zachowaniem hiperelastycznym.

Do tej pory większość analiz zajmujących się hiperelastycznością próbuje znaleźć właściwą funkcję dla swobodnej energii Helmholtza i wyprowadzić odpowiadające jej relacje/zależności naprężenie-odkształcenie oraz sprawdzić je z danymi otrzymanymi z badań/testów [4]-[19]. W niniejszej pracy zastosowano inne podejście.

Tworząc całkę z naprężenia w odniesieniu do odpowiedniego odkształcenia [naprężenie i odkształcenie zgodnie z danymi z badań], można otrzymać przebieg swobodnej energii Helmholtza w zależności od odkształcenia.

Przebieg energii w odniesieniu do badań jedno- i równoosiowych (equibiaxial – równomiernych na wielu osiach odkształcania) ogranicza obszar, w którym może znajdować się energia o wartości uzyskanej w wyniku badań.

Dodatkowo rozkład energii względem rozciągania planarnego (planar tension) daje informację o krzywiźnie funkcji swobodnej energii Helmholtza, która z założenia jest funkcją trójwymiarową, zależną od pierwszego i drugiego niezmiennika (invariant) tensora z prawa ciągłości Cauchy’ego [10].

W pewnych warunkach (niewielkie odkształcenie i 10-krotnie większa szerokość próbki od jej grubości) test rozciągania płaskiego jest tożsamy z testem czystego ścinania.

2. Ogólna teoria
Ogólnie rzecz biorąc, hiperelastyczność jest uogólnieniem sprężystości liniowej, w celu uchwycenia nieliniowych relacji naprężenie-odkształcenie, z pominięciem efektów lepkosprężystości [tj. oddzialywania chwilowego].

Z równań pola i praw równowagi [zachowanie masy, zachowania pędu liniowego i kątowego, zachowania energii oraz I i II zasady termodynamiki] można wyprowadzić równania konstytutywne dla materiału termoelastycznego.

Materiał taki można scharakteryzować za pomocą wektora strumienia ciepła, tensora naprężeń Cauchy’ego σ, energii wewnętrznej na jednostkę objętości oraz entropii na jednostkę objętości, a wszystko to w zależności od gradientu odkształcenia F, temperatury i gradientu temperatury [11].

W badaniach opisanych w dalszej części artykułu temperatura oraz gradient temperatury były utrzymywane na stałym poziomie. W związku z tym naprężenie Cauchy’ego σ, które jest przedmiotem dalszych rozważań, zależy tylko od gradientu odkształcenia i może być wyprowadzone z funkcji energii swobodnej Helmholza ψ (C) [11].

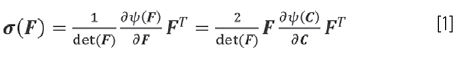
Dla izotropowego modelu hipersprężystego energia swobodna Helmholza jest często wyrażana za pomocą inwariantów/ niezmienników tensora C z prawa Cauchy’ego-Greena. Dla materiału nieściśliwego [objętość v – w aktualnej konfiguracji równa się objętości V – w konfiguracji odniesienia] trzeci inwariant/niezmiennik I3 wynosi jeden, dlatego w dalszej części opisu analiza/rozważanie ogranicza się do dwóch pierwszych inwariantów/niezmienników I1, I2.

W ogólności te trzy niezmienniki dają zależności [11].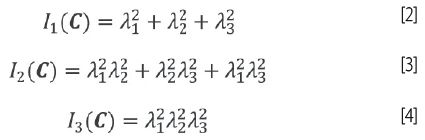

Używając wyrażenia w postaci niezmienników I1, I2, I3 do sformułowania funkcji energii swobodnej Hemholtza ψ (C), naprężenia Cauchy’ego σ, w zależności od tensora C z prawa Cauchy’ego-Greena prowadzi do [11]:

^{1 Energia swobodna Helmholtza (F [a]) – funkcja stanu (zależna wyłącznie od stanu układu, czyli od aktualnych wartości jego parametrów, takich jak masa, liczność materii, temperatura, ciśnienie, objętość i inne) i potencjał termodynamiczny odpowiadający tej części energii wewnętrznej, która może być w danym procesie uwolniona na zewnątrz układu w formie pracy lub ciepła przy stałej temperaturze i objętości.}

^{Jest to przydatna funkcja, w odróżnieniu od energii wewnętrznej, można ją łatwo wyznaczyć, gdyż zależy w sposób naturalny od temperatury, objętości i liczby moli substancji, a parametry te można łatwo mierzyć.}

Zależność/relacja ta posłuży do wyznaczenia naprężeń w odniesieniu do odpowiedniej funkcji energii swobodnej Helmholtza. W niniejszej pracy/artykule wykorzystano opisane we wstępie badania, aby uzyskać pierwsze oszacowanie, jak wygląda funkcja energii w przypadku akustycznej folii PVB.

Dlatego w pierwszym kroku należy wyprowadzić wszystkie odpowiednie gradienty deformacji F i tensory C z prawa Cauchy’ego-Greena, aby wyrazić energię w płaszczyźnie niezmienników. Wartości gradientu deformacji F są charakteryzowane przez odpowiednie odcinki λi, które są zdefiniowane/określone jako:

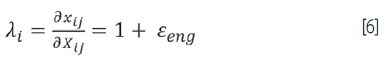
Rozciąganie jednoosiowe

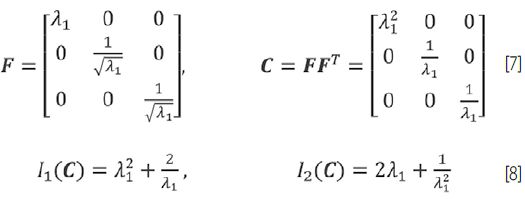
Rozciąganie dwuosiowe

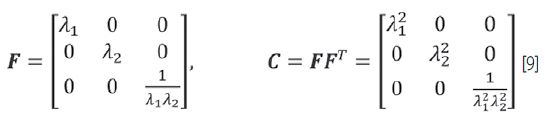
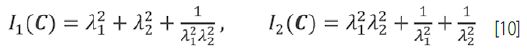
Rozciąganie planarne

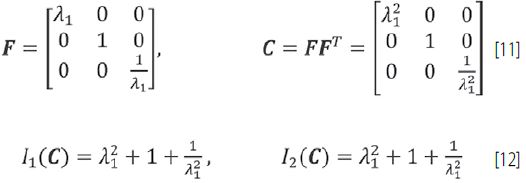
Odpowiednia energia jest obliczana w następujący sposób:

Analityczna ocena tego wyrażenia wykraczałaby poza zakres niniejszego artykułu i dlatego jest odłożona do następnych publikacji autorów. W kontekście niniejszego artykułu funkcja energii jest otrzymywana poprzez numeryczne całkowanie danych zebranych doświadczalnie odnośnie relacji naprężenie-odkształcenie:

gdzie całkowanie przeprowadza się numerycznie na jednostkę objętości przy użyciu reguły trapezu:

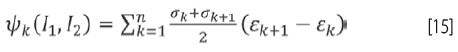
3. Procedura badawcza
Próbki materiału międzywarstwy (folii laminującej) Saflex QS41 zostały dostarczone przez Eastman Chemical Company. Każda próbka przed badaniem była kondycjonowana w komorze klimatycznej przez co najmniej 24 godziny w temperaturze 23oC i wilgotności względnej 50%.

Badania przeprowadzono przy quasi-statycznej prędkości przesuwu poprzeczki 10 mm/min w laboratorium Instytutu Inżynierii Budowlanej (Institute for Structural Engineering) na Uniwersytecie Bundeswehry w Monachium w temperaturze 23±1°C.

Odkształcenie mierzono za pomocą systemu DIC [Cyfrowa Korelacja Obrazu – Digital Image Correlation]. W celu zapewnienia zgodności pomiędzy stopniami obciążenia i odkształcenia, czujnik obciążenia został sprzężony/połączony z DIC poprzez sygnał analogowy, a obie częstotliwości pomiarowe zostały wybrane jednakowo.

Na próbkę naniesiono (metodą natrysku) wzór stochastyczny, który został zarejestrowany przez program GOM Aramis. Każdy punkt wzoru jest śledzony przez całą procedurę badawczą, a odpowiednie pole przemieszczenia dla każdego kroku jest rejestrowane.

Aby ocenić odpowiednie odkształcenia, wybierane są istotne/zauważalne punkty i oceniane za pomocą skryptu/algorytmu MATLAB. Punkty, które zostały wybrane do oceny są pokazane na rysunku 1-3.

Odkształcenia inżynierskie obliczane są poprzez określenie położenia przeciwległych punktów w kolejnych krokach czasowych i porównanie ich z odległością pierwszego kroku [12]:

Wyniki naprężeń są obliczane poprzez podzielenie zmierzonej siły przez pole powierzchni odpowiednich przekrojów poprzecznych.

W rozdziale 4 wybrano następujące modele - odkształcenie Greena-Lagrange- ’a i drugie naprężenie Piola-Kirchoffa do oceny funkcji energii swobodnej Helmholtza z wykorzystaniem danych otrzymanych w badaniach.

Na poniższych rysunkach pokazano rozmiary (przedstawiono wymiary) [oprócz rysunków, wszystkie próbki mają grubość nominalną 0,76 mm] oraz wykresy odkształceń dla trzech badań. Szare obszary jakościowo odzwierciedlają/przedstawiają obszary jednorodnych naprężeń, gdzie gradienty odkształceń, jak określono powyżej, są prawdziwe w dobrym przybliżeniu. Próbki zostały ukształtowane zgodnie z zaleceniami podanymi w publikacjach [13] i [14].

Rozciąganie jednoosiowe

Rys. 1. Odkształcenie wzdłużne w konfiguracji referencyjnej/odniesienia i przy dwóch różnych krokach czasowych

Rozciąganie dwuosiowe

Rys. 2. Odkształcenie główne w konfiguracji referencyjnej/odniesienia i w późniejszym kroku/etapie czasowym

Rozciąganie planarne

Rys. 3. Odkształcenie poprzeczne w konfiguracji referencyjnej/odniesienia i w późniejszym kroku/etapie czasowym

Podczas badań, naprężenia i odkształcenia mogły być bardzo dobrze wychwycone przez DIC i czujnik siły nawet dla przypadków dużych odkształceń. W następnym rozdziale przedstawiono ocenę wyników w odniesieniu do swobodnej energii Helmholtza.

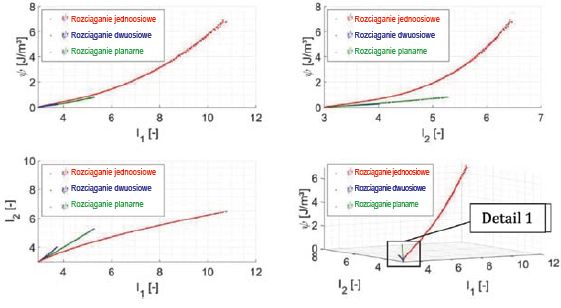
Rys. 4. Swobodna energia Helmholtza ψ wyrażona w kategoriach/postaci dwóch pierwszych niezmienników I1, I2 dla Saflex QS41

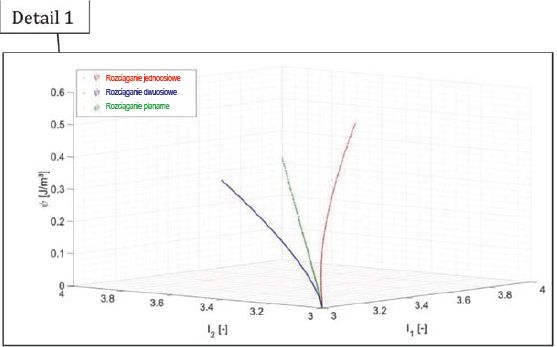
Rys. 5 Początek rozkładu energii swobodnej Helmholza ψ wyrażonej w postaci dwóch pierwszych niezmienników I1, I2 dla Saflex QS41

4. Wyniki badań
Na kolejnych rysunkach swobodna energia Helmholtza, otrzymana w sposób opisany w rozdziale 3, jest przedstawiona w postaci inwariantów/niezmienników tensora Cauchy-Greena.

W celu oceny dopasowania powszechnie stosowanej funkcji swobodnej energii Helmholtza zastosowano model konstytutywny Mooney-Rivlina [15]

oraz funkcję wielomianową,

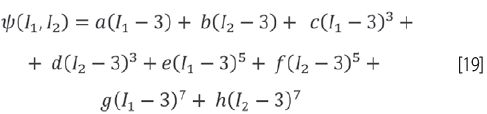
która jest kalibrowana na podstawie dostępnych danych otrzymanych w badaniach i przedstawione graficznie na rys. 5 i 6.

Jak można zauważyć, model konstytutywny Mooney-Rivlin jest gorzej przystosowany do reprezentowania funkcji swobodnej energii Helmholtza w porównaniu z funkcją wielomianową. Jednak nawet podejście wielomianowe nie oddaje dobrze wyników ścinania dwuosiowego i czystego. Potwierdza to tezę zawartą we wstępie, że należy opracować bardziej odpowiednią postać funkcji swobodnej energii Helmholtza dla PVB.

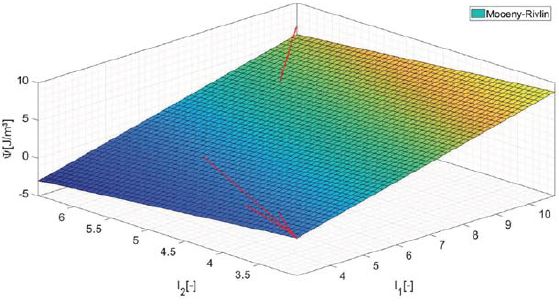
Rys. 6. Funkcja energii swobodnej Helmholtza według Mooney-Rivlina

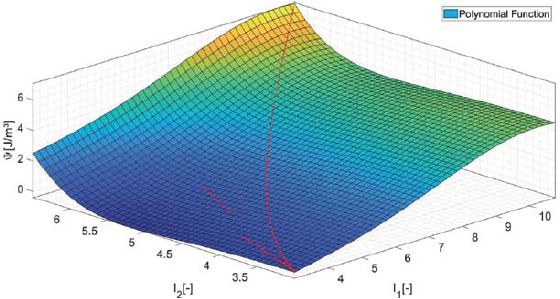
Rys. 7. Energia swobodna Helmholtza dopasowana przez funkcję wielomianową

5. Wnioski
W niniejszym artykule przeprowadzono proste numeryczne całkowania danych eksperymentalnych (otrzymanych w przeprowadzonych badaniach) dotyczących naprężeń w celu uzyskania swobodnej energii Helmholtza, a wyniki dla jednoosiowego, dwuosiowego i planarnego rozciągania zilustrowano w odniesieniu do pierwszych trzech niezmienników.

Stwierdzono, że powszechnie stosowane funkcje, takie jak model Mooney-Rivlina nie oddają dobrze zmierzonej (czyli określonej przez wyniki wynikające z badań) powierzchni swobodnej energii Helmholtza.

Podsumowując z jednej strony, należy przeprowadzić więcej badań, aby otrzymać statystycznie bardziej znaczące/istotne wyniki, a z drugiej strony – dla międzywarstw (folii laminujących) z PVB do szkła laminowanego, należy wyprowadzić analityczne rozwiązanie dla wyrażenia pojedynczych energii dla każdego badania, jak również dla całego materiału.

Alexander Pauli, Michael A. Kraus, Gerald Siebert

Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. w Tampere w Finlandii

Literatura
[1] Kraus, M. A., i M. Niederwald. Uogólniona metoda kolokacji z wykorzystaniem macierzy sztywności w kontekście teorii lepkosprężystości liniowej (Generalized collocation method using Stiffness matrices in the context of the Theory of Linear viscoelasticity (GUSTL)). Tech. Mech 37.1 (2017): 82-106.
[2] Botz, Martin, Michael A. Kraus, i Geralt Siebert. Analiza wrażliwości dla wyznaczania modułu ścinania dla międzywarstwy w szkle laminowanym z zastosowaniem badania skręcania (Sensitivity analysis for the determination of the interlayer shear modulus in laminated glass using a torsional test). Glass Structures & Engineering 3.2 (2018): 355-371.
[3] Schuster, Miriam, i in. Badania termoreologicznie złożonego zachowania materiałowego międzywarstwy etylen-octan winylu w bezpiecznym szkle laminowanym (Investigations on the thermorheologically complex material behaviour of the laminated safety glass interlayer ethylene- vinyl-acetate). Glass Structures & Engineering 3 (2018): 373-388.
[4] Treloar, L. R. G. Elastyczność sieci cząsteczek o długim łańcuchu - I (The elasticity of a network of long-chain molecules- I). Transactions of the Faraday Society 39 (1943): 36-41.
[5] Treloar, L. R. G. . Elastyczność sieci cząsteczek o długim łańcuchu – II (The elasticity of a network of long-chain molecules-II). Transactions ofthe Faraday Society 39 (1943): 241-246.
[6] Rivlin, RSl. Duże odkształcenia sprężyste materiałów izotropowych. I. Pojęcia podstawowe (Large elastic deformations of isotropic materials. I. Fundamental concepts). Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 240.822 (1948): 459-490.
[7] Ogden, Raymond William. Izotropowa elastyczność dla dużych odkształceń – korelacja teorii i eksperymentu dla nieściśliwych materiałów gumopodobnych. (Large deformation isotropic elasticity– on the correlation of theory and experiment for incompressible rubberlike solids). Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 326.1567 (1972): 565-584.
[8] Drass, M., J. Schneider, and S. Kolling. Nowatorska wolumetryczna funkcja energii swobodnej Helmholtza uwzględniająca izotropową kawitację przy skończonych odkształceniach (Novel volumetric Helmholtz free energy function accounting for isotropic cavitation at finite strains). Materials & Design 138 (2018): 71-89.
[9] Drass, Michael, Miriam Schuster, i Jens Schneider. Porównanie niekonwencjonalnych metod badawczych do charakterystyki mechanicznej materiałów polimerowych w nowoczesnych konstrukcjach szklanych (Comparison of unconventional testing methods for mechanical characterization of polymeric materials in modern glass structures). IABSE Symposium Report. Vol. 109. No. 27. International Association for Bridge and Structural Engineering, 2017.
[10] Diebels, S., i in. Mechanika Eksperymentalna: Od pomiaru do modelu materiału (Experimentelle Mechanik: Von der Messung zum Materialmodell.) Rundbrief GAMM (2015).
[11] Bergstrom, Jorgen S. Mechanika polimerów stałych: teoria i modelowanie obliczeniowe (Mechanics of solid polymers: theory and computational modeling). William Andrew, 2015.
[12] Kraus, Michael A., i in. Metody identyfikacji parametrów dla modeli materiałów lepko- i hiperelastycznych (Parameter identification methods for visco-and hyperelastic material models). Glass Structures & Engineering 2.2 (2017): 147-167.
[13] Seibert, H., T. Scheffer, i S. Diebels. Badanie dwuosiowe elastomerów - konfiguracja doświadczalna, pomiary i eksperymentalna optymalizacja kształtu próbki (Biaxial testing of elastomersexperimental setup, measurement and experimental optimisation of specimen’s shape). Technische Mechanik 34.2 (2014): 72-89.
[14] Vöhringer, M., i E. Haberstroh. Metoda wyznaczania parametrów materiałowych: Symulacja złożonych stanów naprężeń w elastomerach (Methode zur Bestimmung der Materialparameter: Simulation komplexer Beanspruchungszustände von Elastomeren).KGK. Kautschuk, Gummi, Kunststoffe 60.6 (2007).
[15] Mooney, Melvin. Teoria dużych odkształceń sprężystych (A theory of large elastic deformation). Journal of applied physics 11.9 (1940): 582-592.

Całość artykułu w wydaniu drukowanym i elektronicznym 

Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne 
Więcej informacji:  Świat Szkła 1/2022