Teoria Griffitha opisuje zachowanie kruchych materiałów. Do opisu powstawania pęknięcia wykorzystuje się równowagę energetyczną. W szkłach odprężonych równowaga ta sprowadza się do prostego wzoru opisującego energię mechaniczną w szkle i energię powierzchniową potrzebną do powstania pęknięć. W artykule postawiono pytanie, czy test upuszczenia kuli na szkło pozwala na wykazanie zasad powstawania pęknięć.
Ponadto właściwa energia powierzchniowa jest współczynnikiem opisującym energię potrzebną do wytworzenia/powstania pęknięć. Dlatego też spróbujemy dokonać analizy tego, czy testy upuszczania kuli dają podobne wartości specyficznej energii powierzchniowej, jak testy statyczne, np. testy podwójnego wspornika lub trzypunktowego zginania. Wyniki badań pokazują stały współczynnik energii powierzchniowej przy różnych wysokościach spadania kuli.
Niemniej jednak zmierzony współczynnik wykazał znaczną różnicę w stosunku do statycznie wyznaczonych współczynników energii powierzchniowej. Wyjaśniono to jedynie częściowym wykorzystaniem energii potencjalnej spadku kuli do powstania pęknięcia.
Dużą rolę w pochłanianiu/absorpcji energii odgrywa tłumienie tafli szkła, która jest podparta w uszczelce.
Ponadto, wpływ twardości uszczelki użytej do badań jest oceniany pod względem rozkładu energii.
W teście spadania kuli ilość energii jest określona, a jej dopływ nie może zostać zatrzymany podczas eksperymentu. Pomimo łatwości wykonania i przetwarzania, test upuszczenia kuli nie wydaje się być odpowiednim badaniem mechanizmu kruchego pękania szkła.
1 Wstęp
Szkło jest uważane za jeden z najbardziej kruchych materiałów, który prawie nie wykazuje odkształceń plastycznych.
To sprawia, że traktowane jest bardzo „delikatnie” w procesie projektowania, ponieważ materiał nie wykazuje żadnych oznak uszkodzenia przed zniszczeniem.
Projektowanie konstrukcji szklanych jest ułatwione dzięki liniowo-sprężystemu zachowaniu materiału szklanego i jego izotropii. Dlatego też powszechnie stosowane podejście do projektowania dotyczy materiału liniowo-sprężystego i dostarcza prostych wzorów do obliczania stanu granicznego nośności.
Jeśli materiały ulegają awarii (zaczynają pękać), sprężysty materiał nie pomaga nam zrozumieć procesu niszczenia. Potrzebujemy raczej odpowiedniej teorii, aby zrozumieć proces niszczenia kruchych materiałów, takich jak szkło.
Pierwszego wyjaśnienia procesu pękania dokonał Griffith (Griffith, 1921), którego teoria jest używana do opisu zachowania się pęknięć i która zajmuje się kilkoma energiami opisującymi wzrost pęknięć w zależności od zastosowanych energii.
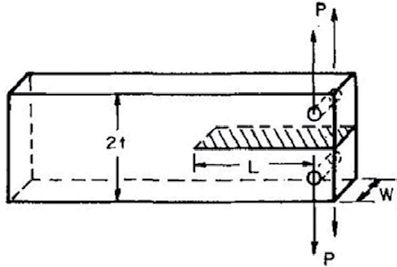
Rys. 1. Technika podwójnego wspornika (Wiederhorn SM, 1969) (Linger i Holloway, 1968)
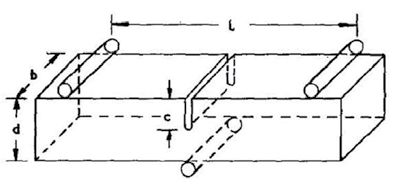
Rys. 2. Zginanie trójpunktowe (Davidge i Tappin, 1968)
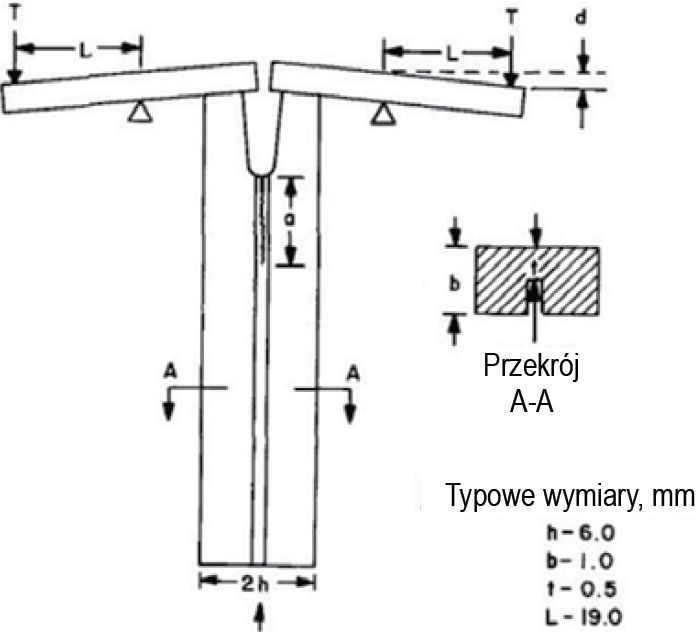
Rys. 3. Zmodyfikowana technika podwójnego wspornika (Davidge i Tappin, 1968)
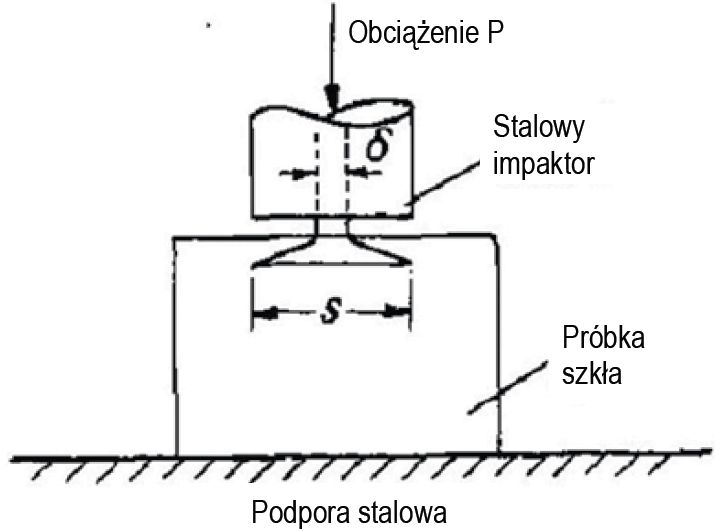
Rys. 4. Impaktor/bijak stożkowy (Roesler, 1956)
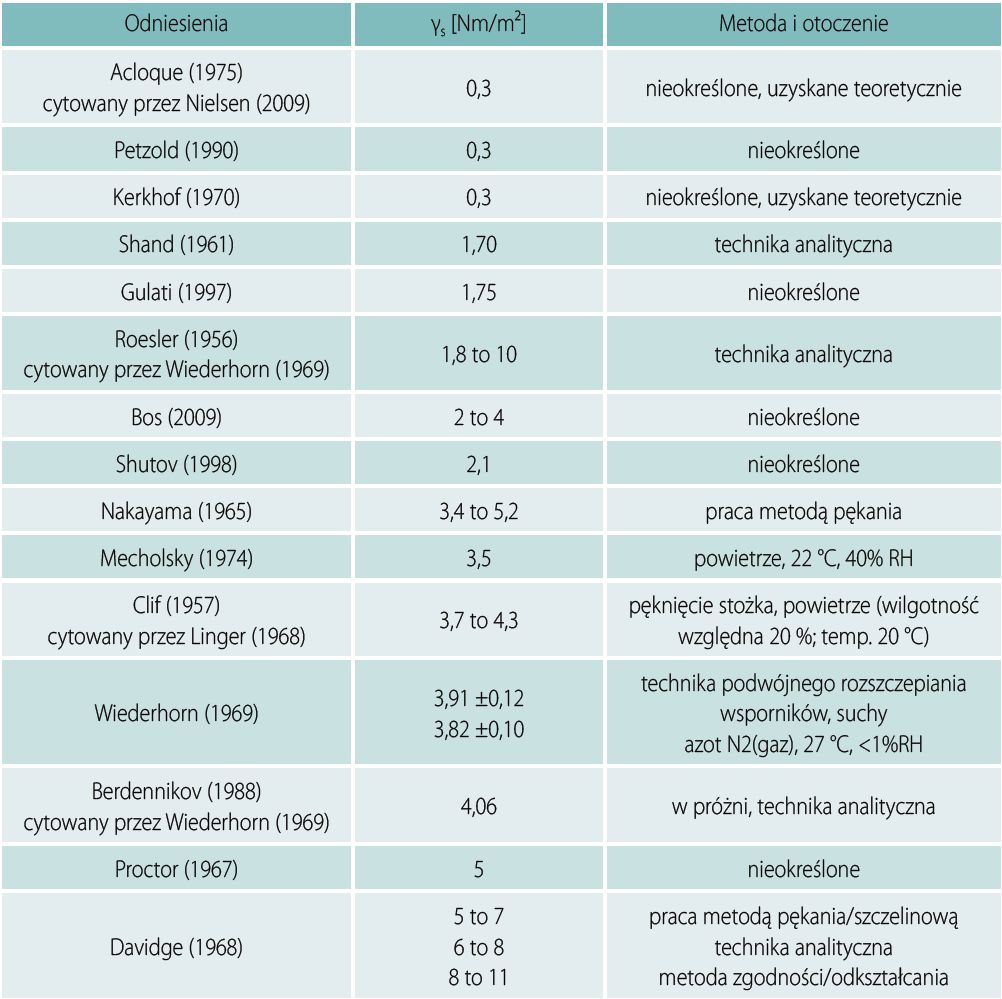
Tabela 1. Energia właściwa powierzchniowa γs szkła sodowo-wapniowego (Reich i Weller, 2012)
2 Równowaga kruchego pękania
2.1 Energetyczne podejście do materiałów kruchych
Opracowano różne teorie opisujące oddziaływanie/interakcję, rozwój i propagację mikroskopijnych i makroskopowych wad (uszkodzeń, rys) prowadzących do pęknięć, mechanizm powstawania dyslokacji i geometrię materiału. Jedną z najbardziej znanych teorii jest koncepcja energetyczna Griffitha (Griffith, 1921), rozwinięta później przez Irvina (Kerkhof, 1970).
Zgodnie z jego podejściem energia potencjalna Upot układu jest sumą energii mechanicznej UM i energii powierzchniowej Uγ powstałej w wyniku propagacji pęknięcia.
Upot = UM – Uγ (1)
gdzie:
Upot to całkowita energia potencjalna układu,
UM to energia mechaniczna,
Uγ to wzrost sprężystej energii powierzchniowej spowodowany tworzeniem się powierzchni pęknięć.
Energia mechaniczna składa się z wewnętrznej energii odkształcenia sprężystego U0 (w tym odkształcenia zewnętrznego – przemieszczenia wywołane przez przyłożoną siłę) zmagazynowanej w sprężystym materiale szkła oraz energii potencjalnej obciążenia zewnętrznego (pracy zewnętrznej), które jest przyłożone do szkła. Równanie 1 może być rozwinięte z wykorzystaniem tych energii.
Przy założeniu pęknięcia bliskiego równowadze, co oznacza pełne przekazanie energii sprężystej na tworzenie pęknięcia i brak zmagazynowanej energii odkształcenia w szkle odprężonym równanie (2), upraszcza się do
Upot = U0 – UE + WE – Uγ (2)
gdzie:
Upot to całkowita energia potencjalna układu,
U0 to energia odkształcenia sprężystego niepękniętej szyby,
Uγ to wzrost sprężystej energii powierzchniowej spowodowany tworzeniem się powierzchni pęknięć,
WE to wykonana praca zewnętrzna.
Przy założeniu pękania bliskiego równowadze, co oznacza pełne przekazanie/przeniesienie energii sprężystej na tworzenie/powstawanie pęknięcia i brak zmagazynowanej energii odkształcenia w szkle odprężonym równanie (2,) upraszcza do
U0 + WE = Uγ (3)
co oznacza, że cała wewnętrzna energia odkształcenia sprężystego U0 i całe obciążenie zewnętrzne WE jest przekazywane i zamienia się w energię powierzchniową.
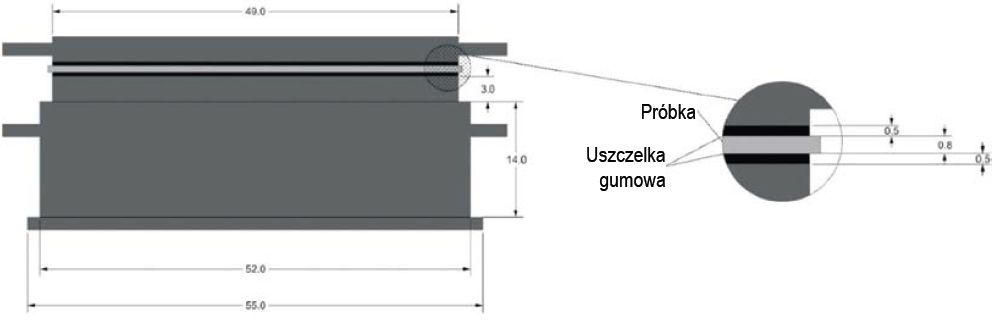
Rys. 5. Układ do badania spadania kuli dla szyb 500 mm x 500 mm zgodnie z DIN 52338 (stosowany do badania produkcyjnego/ fabrycznego bezpiecznego szkła laminowanego) (Vanapalli 2014)

Rys. 6. Typowe pęknięcie nie jest płaskie, dlatego jego długość pomnożono przez 1,15 (Vanapalli 2014)
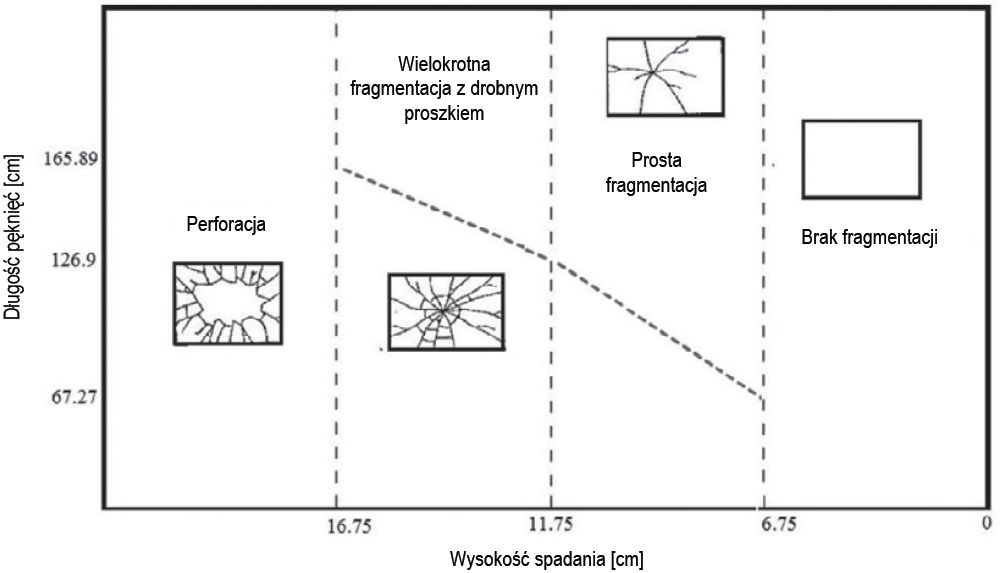
Rys. 7. Schemat przebiegu pękania w odniesieniu do wysokości upadku kuli stalowej o masie 1000 g i średniej długość pęknięcia (Vanapalli 2014)
Tabela 2. Średnie wyniki z kulą stalową 1000 g przy szkle 8 mm, szkło ułożone w uszczelkach gumowych

2.2 Energia odkształcenia sprężystego U0 i praca odkształcenia WE
Energia odkształcenia sprężystego U0 i praca odkształcenia WE zawierają całą energię, która jest zmagazynowana lub przyłożona do szyby i może być wykorzystana do powstania i wzrostu pęknięć.
Energia odkształcenia sprężystego jest typowo (odpuszczanie termiczne) przyłożonym obciążeniem. Obciążenie przyłożone do ciała liniowo sprężystego odkształca to ciało proporcjonalnie do obciążenia. Całkowitą energię odkształcenia sprężystego ciała uzyskuje się przez całkowanie gęstości energii odkształcenia X (x,y,z) po objętości ciała.
Jest ona magazynowana w ciele w postaci równoważnej ilości energii – energii odkształcenia sprężystego (pierwsza zasada termodynamiki). Obciążenie przyłożone do ciała liniowo sprężystego odkształca to ciało proporcjonalnie do obciążenia. Równania (4) i (5) obowiązują dla materiałów podlegających prawu Hooke’a.
X (x,y,z) = ½ εσ (4)
UE = ∫ X(x,y,z) dxdydz = ΣσijεijΔV (5)
gdzie
Χx,y,z to gęstość odkształcenia.
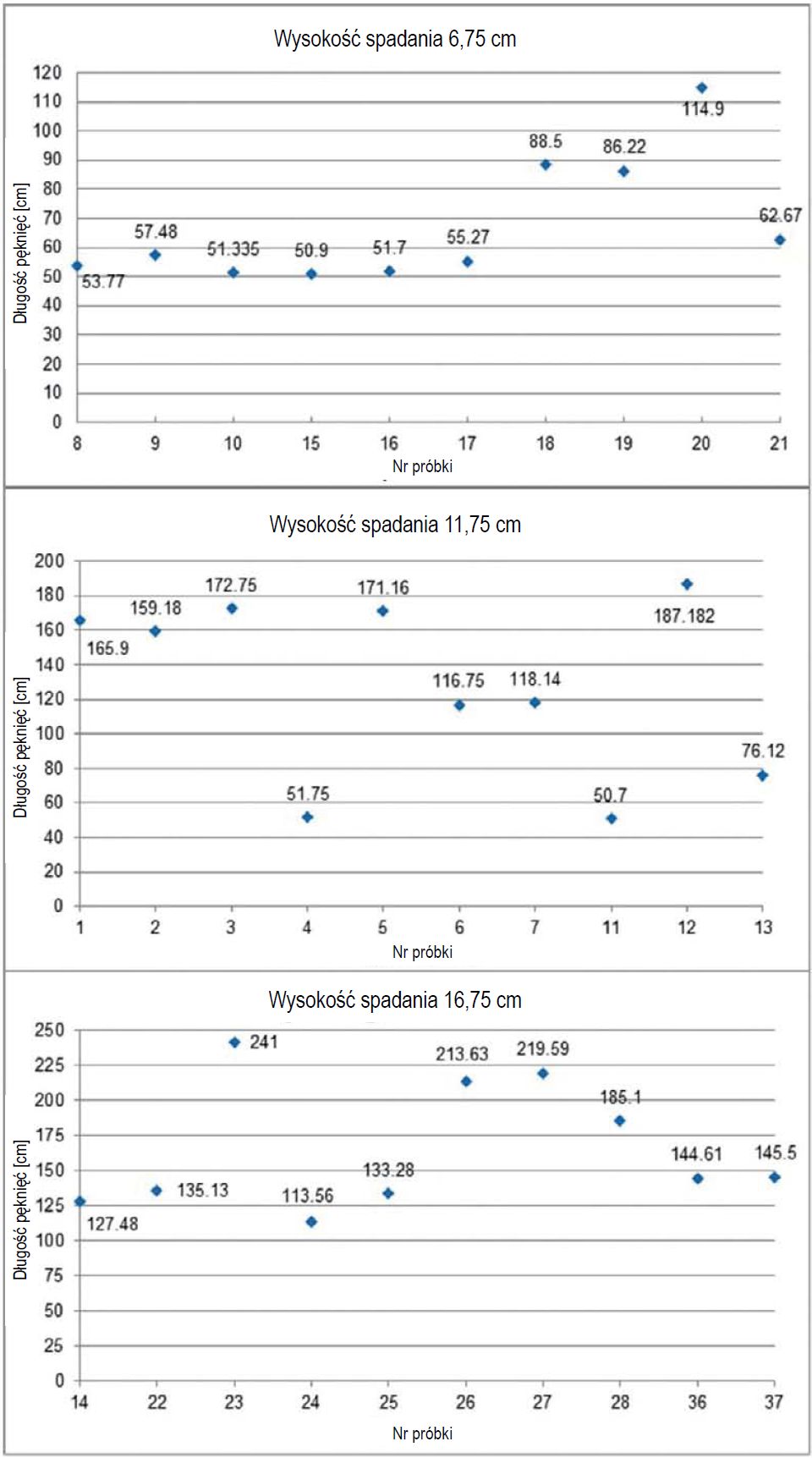
Rys. 8: Długość pęknięcia w zależności od wysokości spadku - 6,75 cm, 11,75 cm i 16,75 cm (Vanapalli, 2014)

Rys. 9. Wzór spękania przy wysokościach spadku 6,75 cm, 11,75 cm i 16,75 cm (Vanapalli, 2014)
2.3 Energia powierzchniowa γs
Rozbicie ciała na dwie lub więcej części wymaga degradacji wiązań (jonowych, atomowych lub molekularnych) pomiędzy składnikami materialnymi. Dlatego siła tworząca wiązanie musi wykonać neutralizującą pracę specyficzną dla materiału. Praca ta to energia powierzchniowa niezbędna do utworzenia nowych powierzchni.
Pęknięcie (rysa, szczelina) tworzy na ogół dwie powierzchnie, tak że energia powierzchniowa Uγ dla jednego pęknięcia jest iloczynem podwójnej energii właściwej powierzchniowej γs, grubości szkła t i długości pęknięcia x (Petzold et al. 1990).
Uγ = 2γsxt (6)
gdzie
γs to właściwa energia powierzchniowa,
t to grubość szkła,
x to długość pęknięcia.
Właściwość materiału γs to energia powierzchniowa wymagana na jednostkę powierzchni pęknięcia. Kilku autorów dopuszcza, że właściwość materiałowa jest stała, ale proponują różne wartości. Tabela 1 podsumowuje wyniki eksperymentalne (γs = 1,7 do 11 Nm/m²), które znacznie różnią się od wartości teoretycznych (γs = 0,3 Nm/m²).
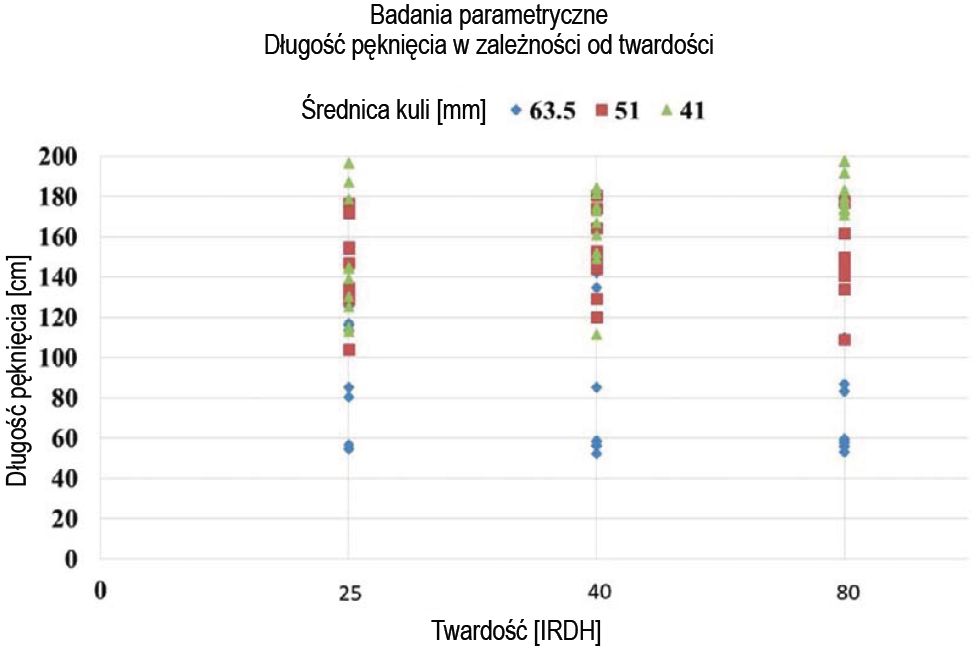
Rys. 10. Analiza parametryczna spadku kuli przy trzech średnicach kuli i trzech twardościach uszczelki
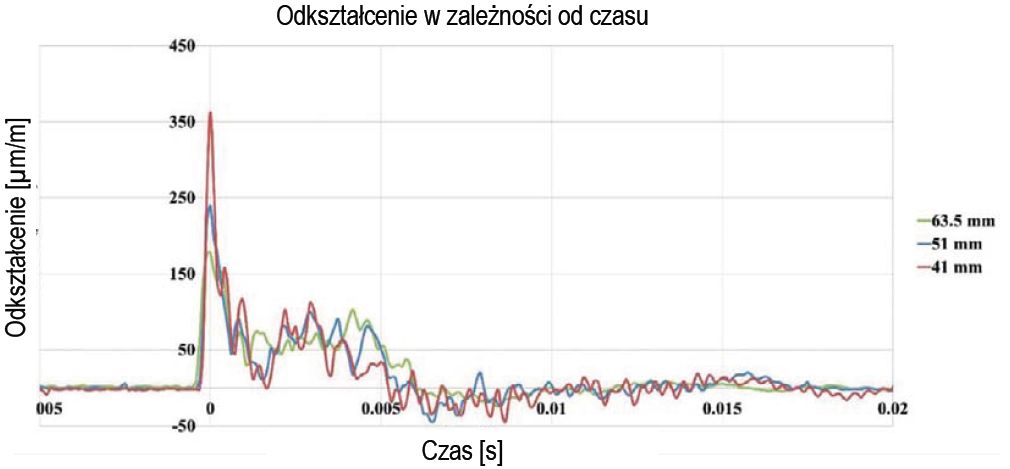
Rys. 11. Odkształcenie w płaszczyźnie spowodowane uderzeniem w badaniach spadania kuli dla trzech średnic kul (63,5 mm, 51 mm, 41 mm)
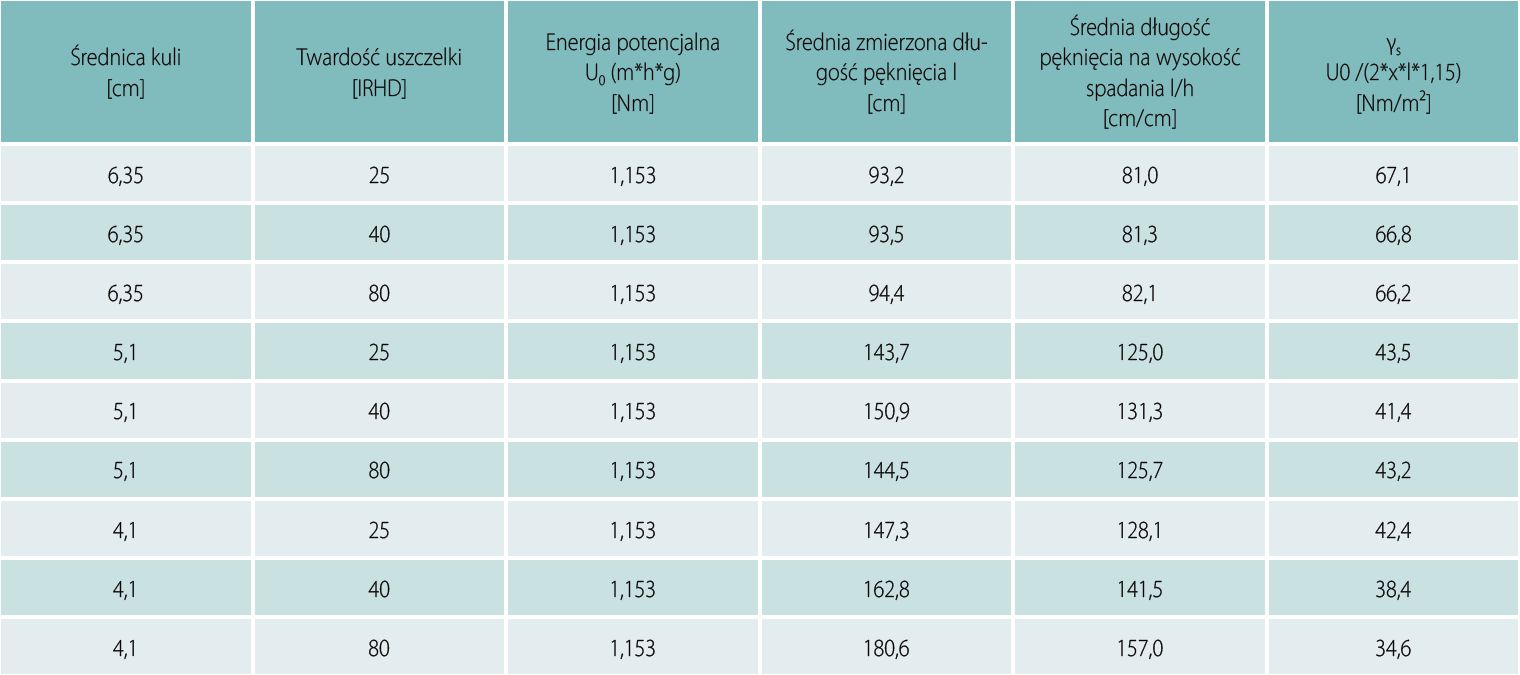
Tabela 3 Średnie wyniki badań parametrycznych przy szkle grubości 8 mm, szkło ułożone na uszczelkach gumowych
2.4 Formułowanie metod określania właściwej energii powierzchniowej γs
Różne wartości energii powierzchniowej właściwej γs, podane w tabeli 1, wyznaczono doświadczalnie. Eksperymenty te opierały się na statycznym przyłożeniu obciążenia. Typowe konfiguracje/układy badawcze obejmowały techniki podwójnego wspornika (rys. 1) lub zmodyfikowane techniki podwójnego wspornika (rys. 3), trzypunktowe zginanie (rys. 2) i impaktor stożkowy (urządzenie udarowe) (rys. 4).
Z porównania tych technik wynika, że zawsze do wyznaczania energii pękania potrzebnej do tworzenia/propagacji pęknięć stosowano zawsze małe próbki o skomplikowanej geometrii. I – co znacznie ważniejsze – we wszystkich badaniach zastosowano zasadę, że powoli przykłada się do próbek określoną siłę i mierzy propagację pęknięcia. W efekcie uzyskuje się wyraźną zależność siła- pęknięcie.
3 Badania efektów spadania kuli w celu określenia energii pękania
3.1 Idee/Pomysły
Zastosowanie znanych technik (rys. 1– rys. 4) wymaga wszechstronnego przygotowania, zwłaszcza wykonanie małych próbek jest czasochłonne i kosztowne. Nie wiadomo, jak proste, dynamiczne badania z dynamiczną skalą żywotności dałyby podobne wyniki.
Celem badań jest wykazanie, że istnieje bezpośrednia zależność pomiędzy energią uderzenia ciała udarowego a powierzchnią pęknięcia, a ponadto, czy wyniki badań pozwoliły na określenie specyficznej energii powierzchniowej, porównywalnej ze znanymi technikami.
3.2 Układ badawczy
W Niemczech produkcja bezpiecznego szkła laminowanego jest stale sprawdzana za pomocą testu spadania kuli na taflę szklaną zgodnie z DIN 52338, który jest najczęściej wykonywanym testem spadania kuli. Zestaw do badań przedstawiono na rys. 5.
Wszystkie próbki wykonane były ze szkła odprężonego o grubości 8 mm i wymiarach 500 mm x 500 mm. Tafle szkła zamocowano w uszczelce gumowej o grubości 5 mm pomiędzy dolną i górną ramą stanowiska badawczego (Rys. 5). Impaktorem (ciałem uderzającym) była stalowa kula o masie 1000 g.
Badano trzy różne wysokości spadania: 6,75 cm, 11,75 cm i 16,75 cm, po 10 próbek z każdej wysokości. Mała rysa o długości 5 cm w środku dolnej powierzchni stanowiła początkowe stadium/źródło pęknięcia (Rys. 6).
Wyniki
Wzór pęknięcia był zupełnie inny przy trzech wysokościach spadku. Rys. 7 pokazuje, że przy upadku z wysokości 6,75 cm rozpoczęło się pękanie porysowanej szyby, a wraz ze wzrostem wysokości spadania liczba pęknięć wzrastała. Co więcej, przy spadku z wysokości 6,75 cm w punkcie uderzenia prawie nie ma pyłu szklanego, podczas gdy przy wysokości 16,75 cm powstało dużo pyłu.
Poniżej przedstawiono długości pęknięć w szybach przy trzech wysokościach upadku. Długości te zostały zmierzone optycznie i obliczone za pomocą programu komputerowego. Pomimo pomiaru długości pęknięcia nie jest znana dokładna powierzchnia pęknięcia, ponieważ pęknięcie nie jest płaskie i prostopadłe do powierzchni (rys. 6).
Ponadto widoczne są liczne drobne odłamki szkła (wiele małych fragmentów szkła) – określane jako pył/proszek szklany – powstający szczególnie w miejscu uderzenia i przy większych wysokościach spadania stalowej kuli. W dalszych obliczeniach zmierzoną długość pęknięcia mnoży się przez 1,15, aby uwzględnić te efekty. Niemniej jednak, do dalszych badań konieczne jest bardziej szczegółowe rozpatrzenie rzeczywistej powierzchni pęknięcia.
W tabeli 2 przedstawiono średnią długość pęknięcia dla każdej wysokości spadania stalowej kuli oraz obliczone współczynniki energii powierzchniowej γs, które wydają się być stałe przy średnich wartościach, ale ze współczynnikiem od 10 do 20 większym niż wyznaczone za pomocą technik badań statycznych.
Pierwsze porównanie podparcia szkła z uszczelką, bez uszczelki i z różnymi średnicami kul wykazało około 50% różnicę w odkształceniach szkła przy stałej energii potencjalnej. Przeprowadzono badanie parametryczne ze stałą energią potencjalną 1,15 Nm z trzema rozmiarami kul i trzema rodzajami uszczelek.
Testowane są kule o średnicy 63,5 mm, 51 mm i 41 mm o masie odpowiednio 1035 g, 537 g i 289 g. Oceniane są trzy uszczelki o grubości 3 mm i twardości 25, 40 i 80 IRDH. Wyniki badań parametrycznych przedstawiono na rys. 10 i w tabeli 3.
Długości pęknięć były stałe przy różnej twardości uszczelek, ale wraz ze zmniejszeniem rozmiaru kul zwiększała się całkowita długość pęknięcia (Rys. 10 i Tabela 3). W miarę zmniejszania się rozmiaru kul, zmniejsza się obszar kontaktu podczas uderzenia, co prowadzi do lokalnego ugięcia w krótkim czasie, powodując większe odkształcenia i dłuższe pęknięcia.
Ten rodzaj lokalnego ugięcia zaobserwowano również w Chaparala et al., 2015. Aby zweryfikować to lokalne ugięcie, zestaw testowy jest zintegrowany z tensometrem do pomiaru odkształceń spowodowanych testem spadania kuli. Liniowy czujnik/tensometr do pomiaru odkształcenia jest podłączony w środku szkła i wykonany jest pomiar przy użyciu systemu pozyskiwania danych (Quantam X) z częstotliwością 9600 Hz.
Z rys. 11 wyraźnie wynika, że odkształcenie wzrasta wraz ze zmniejszeniem średnicy przy stałej energii. Odkształcenie powstałe w wyniku upadku kuli o średnicy 41 mm jest dwukrotnie większe niż odkształcenie powstałe w wyniku upadku kuli o średnicy 63,5 mm. To wyjaśnia przyczynę wyższego współczynnika powierzchniowego w tabeli 3.
Widać więc, że rozmiar kuli odgrywa istotną rolę podczas uderzenia. Ze względu na ograniczenia sprzętu, prędkość po uderzeniu nie jest mierzona. Do dalszych badań nad wymianą energii proponuje się zmianę momentu podczas uderzenia.
5 Dyskusja i wnioski
Na podstawie przeprowadzonych badań sformułowano następujące wnioski:
- Poprzednie artykuły opisują zastosowanie statycznej techniki badań do wyznaczenia przyłożonej siły i długości pęknięcia oraz wymagają skomplikowanych próbek o małych rozmiarach.
- W testach upadku kuli określono liniową zależność pomiędzy wysokością upadku a długością pęknięcia przy średnich wartościach.
- Współczynniki energii powierzchniowej γs są stałe dla różnych wysokości spadania, ale od 10 do 20 razy większe niż wartości wyznaczone za pomocą technik statycznych i pokazują, że większość energii potencjalnej impaktora (urządzenia uderzającego) nie jest wykorzystywana do tworzenia pęknięć.
- Szczególnie przy dużych wysokościach spadania ilość małych fragmentów szkła (proszek) ma powierzchnię, która nie jest uwzględniona w mierzonej powierzchni pęknięcia i musi zostać dokładniej określona.
- Inne kwestie związane z energią nie są mierzalne, np. czy pęknięcie sięga krawędzi, dźwięk przy pęknięciu szyby, sprężyste zachowanie się tafli szkła.
- Rozmiar kuli odgrywa znaczącą rolę w powstawaniu pęknięć, użycie większej kuli o niższej energii pozwala kontrolować wymianę energii.
- Do obliczenia wymiany energii potrzebna jest zmierzona prędkość kuli po pierwszym uderzeniu.
- W chwili obecnej test spadania kuli nie jest odpowiedni do określenia energii pękania szkła, ponieważ zarówno określenie powierzchni pęknięcia, jak i energii tworzenia pęknięć nie jest możliwe do określenia przy użyciu stosowanego zestawu badawczego. Konieczna jest wiedza, jaki procent energii potencjalnej impaktora jest wykorzystywany do tworzenia/ powstania pęknięć.
Podziękowania
Szczególne podziękowania należą się firmie Thiele Glas Werk GmbH, Wermsdorf, Niemcy, która sponsorowała wszystkie próbki szkła do badań.
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. w Tampere w Finlandii
Sagar Vanapalli, Stefan Reich
Bibliografia
– Acloque, P., 1975. Odkształcenia i pęknięcia szkieł (Deformation et rupture des verres). Ann Mines. 2, pp: 57-66.
– Berdenikov, W. P. 1933. Pomiar napięcia powierzchniowego ciał stałych (Measurement of Surface Tension of Solids). Soviet Phys. Z.S., 4, pp: 397-419.
– Chaparala, S., L. Xue, D.Yu, S. Park, 2015. Zachowanie się dynamiki płaskich płyt szklanych w warunkach uderzenia: eksperymenty i modelowanie numeryczne (Dynamics behavior of flat glass panels under impact conditions: Experiments and numerical modeling), Journal of the Society of Glass, 23, pp: 91-137
– Clif, C. J. 1957. Pęknięcie szkła pod wpływem różnych cieczy i gazów (Fracture of glass under various liquids and gases). Journal of the Society of Glass, 41, pp: 157-167.
– Davidge, R. W. and G. Tappin, 1968. Efektywna energia powierzchniowa materiałów kruchych (The Effective Surface Energy of Brittle Materials). Journal of Materials, 3, pp: 165-173.
– DIN 52338. Metody badań dla szkła płaskiego w budynkach: test spadania kuli dla szkła laminowanego (Test methods for falt glass in buildings: ball drop test for laminated glass), 09/1985.
– Griffith, A.A., 1921. Zjawiska pękania i płynięcia w ciałach stałych (The phenomena of rupture and flow in solids). Philosophical Transactions of the Royal Society London Series A, 221, pp: 163-198.
– Gulati, S. T., 1997. Kruchość hartowanych tafli ze szkła sodowo- wapniowego (Frangibility of Tempered Soda- Lime glass Sheet). Proceedings of Glass Processing Days. Tampere, pp: 227-231.
– Kerkhof, F. 1970. Procesy pękania w szkle (Bruchvorgange in Glasern). Frankfurt am main : Verlag der deutschen glastechnischen Gesellschaft.
– Linger, K. R. and D.G. Holloway 1968. Energia pękania szkła (The Fracture Energy of Glass). Philosophical Magazine, 18, pp: 156.
– Mecholsky, J. J., R.W. Rice and S.W. Freiman, 1974. Przewidywanie energii pęknięcia i wielkości rys/wad w szkle (Prediction of Fracture Energy and Flaw Size in Glasses). Journal of the American Ceramic Society, 57(10), pp: 440-443.
– Nakayama, J., 1965. Bezpośredni pomiar energii pękania idealnych materiałów niejednorodnych (Direct measurement of fracture energies of britlle heterogeneous materialsI). Journal of the American Ceramic Society, 48.11, pp. 583-587.
– Nielsen, J. H., J.F. Olesen and H. Stang, 2009. Pękanie hartowanego szkła sodowo-wapniowo-krzemianowego (The Fracture of Tempered Soda-Lime-Silica Glass. Experimental Mechanics,49(6), pp: 855-870.
– Petzold, A., H. Marusch, and B. Schramm, 1990. Szkło jako materiał budowlany (Der Baustof Glas). Berlin: Verlag fur Bauwesen.
– Proctor, B. A., I. Whitney and J.W. Johnson, 1967. Siła stopionych krzemianów (The strength of fused silica), Proceedings of the Royal Society of London, 297, pp: 534-557.
– Reich, S., B. Weller, N. Dietrich and S. Pfefferkorn, 2012. Energetyczne podejście do energii odkształcenia sprężystego szkła hartowanego termicznie (Energetic approach of elastic strain energy of thermally tempered glass). Challenging Glass. Conference on Architectural and Structural Applications of Glass, Delft, pp: 249-256.
– Roesler, F.C, 1956. Kruche pękanie bliskie równowagi (Brittle Fractures near Equilibrium). Proceedings of the Physical Society of London, 69B, pp: 981-992.
– Shand, E. B., 1961. Korelacja wytrzymałości szkła z wadami pęknięć o zmierzonej wielkości (Correlation of Strength of Glass with Fracture flaws of Measured Size). Journal of the American Ceramic Society, Vol. 44(9), pp: 451-455.
– Shutov, A.I, P.B. Popov and A.B. Bubeev, 1998. Przewidywanie charakteru pękania szkła hartowanego (Prediction of the character of tempered glass fracture). Glass and Ceramics, 55.
– Takahashi, K., 1999. Szybkie pękanie w szkle hartowanym (Fast Fracture in Tempered Glass). Key Engineering Materials, 1999.
– Vanapalli, M.R.S., 2014. Korelacja między energią uderzenia a energią powierzchniową szkła odprężonego (Correlation between impact energy and surface energy at annealed glass). Technical University of Dresden, Dresden.
– Wiederhorn, S. M., 1969. Energia powierzchniowa pękania szkła (Fracture Surface Energy of Glass). Journal of the American Ceramic Society, 55, pp: 99-105.

Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 12/2022































