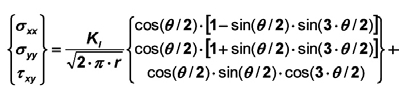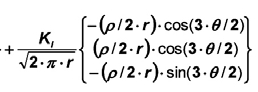In several standards such as EN 1288 test scenarios for the determination of strength of glass is described. On the one hand there is the ring-on-ring test for the determination of the strength of glass without and on the other hand there is the four-point-bending test for the determination of the strength of glass with the influence of the edge strength. All these tests are described having perfect conditions.
For example, glass is homogeneous or test set-ups are without any imperfections. One interesting part is the distribution of the residual stress through the thickness and along the surface. Residual stress is caused by thermal or chemical pre-stress of glass.
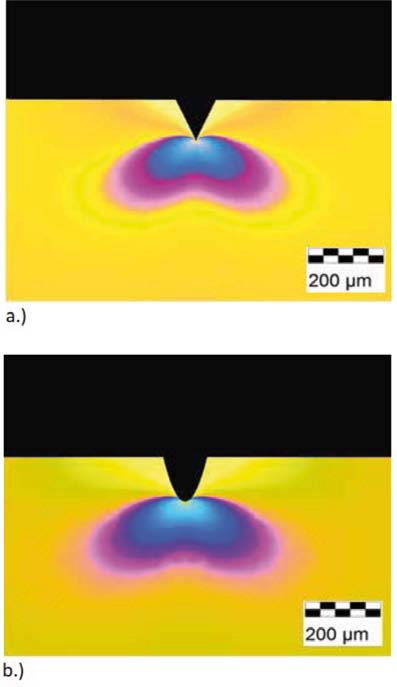
In case of heat strengthened or fully tempered glass photo-elastic studies of the stress distribution showed that the distribution along the surface is not homogeneous.
This not constant distribution is shown in a grey pattern, which can be visualized with the principle of polarized light.
This paper is a discussion about this grey pattern, imperfections and measured stress with the help of SCALP stress measurement device.
This investigation helps to understand much better the reason of the location of the origin of fracture.
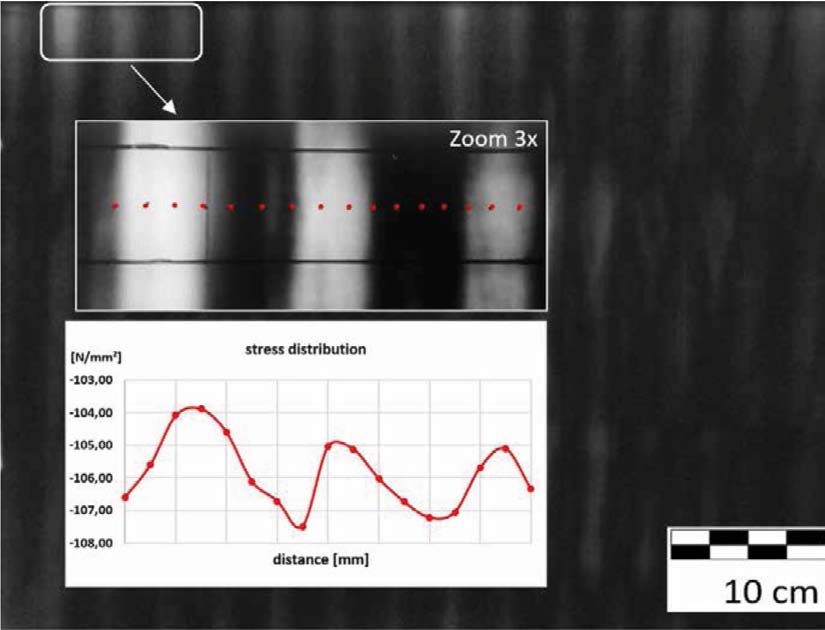
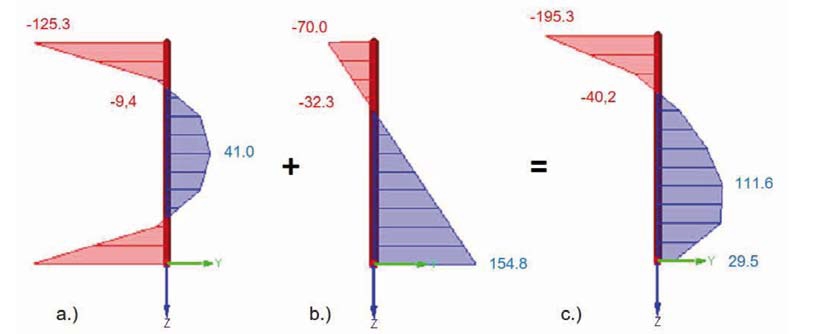
Fig. 1. Distribution of residual stress of fully tempered glass
Introduction
Thermal treatment
Thermal treatment is a typical process of pre-stressing, according EN 12150 [1] or EN 1263 [2], of glass in which the glass is moved on rollers forwards into the heating zone and is heated up above the transition point.
After this heating phase, the glass is blown off with air. During the phase of cooling to ambient temperature, glass is permanently moved forwards and back-wards on rollers up to the end of the furnace.
The thinner the glass the bigger so-called roller waves can occur. For this reason, the Austrian company LISEC has investigated a process in which the glass is transported on air cushion. This technique gives the possibility to pre-stress thinner glass by thermal treatment without roller waves.
Chemical treatment – Ionic Exchange
Another possibility to pre-stress the glass is chemical treatment according EN 12337 [3]. The glass is immerged into molten potassium nitrate.
At a temperature of approx. 370 - 450°C the effect of ionic exchange takes place.
The smaller sodium ions diffuse from the glass into the liquid potassium nitrate and the larger potassium ions penetrate into the glass matrix.
Due to the larger ionic diameter of potassium ions, compressive stresses in the close up range of the surface result. The depth of penetration the so-called case depth is around 30 – 100 μm. [4]
Test scenarios for determination
of ultimate bending strength
In case of thin glass with a thickness less than 2 mm the values for ultimate bending strength, which are the basis for a structural design, are still missing.
Therefore, a couple of different test scenarios were investigated for their applicability for determination of ultimate bending strength of thin glass.
Due to the application one has to differ between test scenarios with and without the influence of the edge strength (edge quality) – the socalled edge effect. In the following a couple of possible test scenarios were investigated.
Ring-on-ring test – EN ISO 1288
The test set-up is performed by placing the glass sample on a circular steel reaction-ring (supporting ring) and applying on its upper surface a load transmitted through a steel loading-ring, until the glass breaks.
The purpose of this test is to achieve a uniform tensile stress field inside of the loading ring that is independent of edge effects. As described in NEUGEBAUER [5] these in EN 1288 described test scenarios fail for thin glass.
Silicon pad / pressure pad
As a possible of improvement of the ring-onring test a silicon-pad or pressure-pad on ring test was investigated.
The test set-up is performed by placing the glass sample on a circular steel reaction ring (supporting ring) and applying on its upper surface a load transmitted through a silicon or pressure pad instead of the loading ring, until the glass breaks.
The advantage of such test setup is that in the centre of the glass a homogenous stress distribution arises. [5]
Four-point bending test
In case of thin glass large deflections result and the bearing forces are not longer vertical but inclined. The glass pane distributes its bearing force only by contact and eventually by friction be-tween glass and rubber (EPDM).
Due to the thinness no breakage of these thin glass panels can eventually be reached, because of slip from bearing pins due to bowstring effect (distance of pins is constant but ends of panes move towards) or on some testing machines reach of maximum piston stroke. [5]
Bending with axial force
The value for the ultimate bending strength can for example be determined with a kind of a stability test. With a force F and eccentricity e the maximum stress can be determined according the theory of large deformations. Instead of inducing bending by loading perpendicular to test specimen an alternative concept applies the load in plane of the test specimen with bending due to deflection. [5]
Bending with constant radius Instead of introducing the load in plane as described above it is also possible to apply the load with a rotation of the shorter opposite edges and a reduction of the distance between the supporting hinges, as described NEUGEBAUER [5].
With an accurate adjustment of the length of bowstring (distance between the supporting hinges) of the arched bent glass sample and the applied rotation a constant stress distribution on nearly the whole bent edges (excluding a small zone at the straight edges where the rotation is introduced) arises. [5]
Stress distribution on surface
Anisotropy
In general, the phenomenon of anisotropy can be defined as a characteristic of the material, that has directionally dependent behaviours of the material for example like tensile strength, conductivity or refractive index.
In case of glass, the anisotropy effect results from the presence of polarized light in the natural environment, the birefringent property the anisotropy of the refractive index of glass (photoelasticity) and mechanical stresses in the glass due to the thermal pre-stressing process. [6].
To understand this behaviour much better prestressed glass was investigated with the help of the physic principle of polarisation. In case of fully tempered glass a so-called “zebra pattern” arises, the picture is shown in figure 1 below.
This 8 mm glass is pre-stressed in a conventional tempering furnace on rollers. In certain points the residual stress on the surface were measured with help of SCALP measurement device.
As shown in the diagram in figure 1 above the measured residual stress in not homogenous along the surface. The level of stress is varying in a range of maximum and minimum. In this case the compressive stress at the surface was measured between s = -102.8 and -107.5 MPa.
For the discussion of the determination of the ultimate bending strength these distributions, caused by tempering processes, have to be taken into account. Not only the distribution along the surface has an influence on the bending strength the distribution through the thickness has to be taken into account as well.
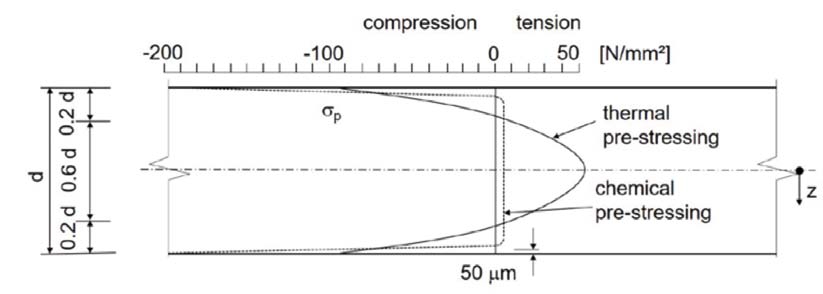
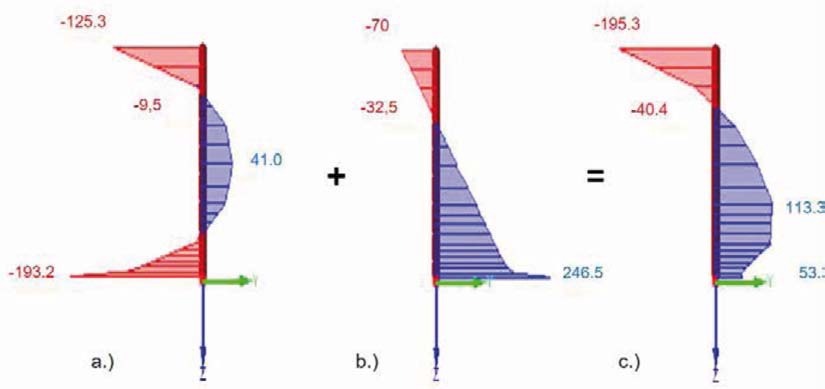
Fig. 2. Distribution of residual stress of thermally and chemically pre-stressed glass
(...)
(...)
Jürgen Neugebauer
University of Applied Sciences FH-Joanneum
Irma Kasumovic
Josef Ressel Centre for thin glass technology for structural glass applications
Ivo Blazevic
Josef Ressel Centre for thin glass technology for structural glass applications
References
[1] EN 12150; Glass in buildings – Thermally toughened soda lime silicate safety glass
[2] EN 1863; Glass in building – Heat strengthened soda lime silicate glass
[3] EN 12337; Glass in buildings – Chemically strengthened soda lime silicate glass
[4] Neugebauer J.; Movable Canopy, conference proceedings, Conference proceedings; Glass Performance Days, Tampere, Finland, 2015
[5] Neugebauer J.; Investigation of different test set scenarios for determination of ultimate bending stress of thin glass; Conference proceedings; Engineered Transparency; Düsseldorf; 2016
[6] Illguth M., Schulera C., Bucak Ö.;The effect of optical anisotropies on building glass façades and its measurement methods; Frontiers of Architectural Research 4; 119–126; Elsevier; 2015
[7] Schula S.; Charakterisierung der Kratzanfälligkeit von Gläsern im Bauwesen; Doctoral Thesis; Darmstadt; 2014
[8] Gross D., Seelig T.; Bruchmechanik; Springer-Verlag Berlin Heidelberg;2011
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 3/2019